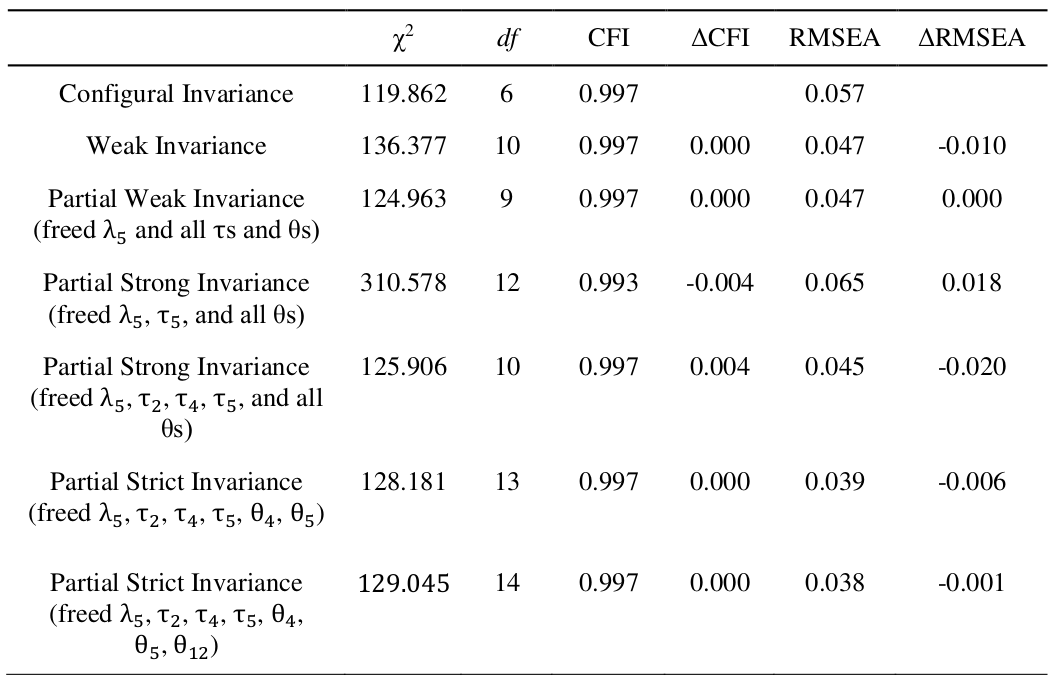
What to Do If Measurement Invariance Does Not Hold?

# What to Do If Measurement Invariance Does Not Hold?
## Let’s Look at the Practical Significance
### Hok Chio (Mark) Lai
### University of Southern California
### September 24, 2021

---

# Abstract

Measurement invariance---that a test measures the same construct in the same way across subgroups---needs to hold for subgroup comparisons to be meaningful. There has been tremendous growth in measurement invariance research in the past decade. However, such research usually only provided binary conclusions of whether invariance holds or not, which gave little practical guidance on subsequent test usages in research and assessment settings. This presentation will illustrate these issues with an in-progress research synthesis of 32 invariance studies of a depression scale across genders. I will then provide suggestions on effect size indices that provide more information on the magnitude of noninvariance, and share a related Bayesian procedure for establishing invariance at the composite score level. Finally, I will discuss a procedure for quantifying how noninvariance affects the test's selection/diagnostic accuracy.

---

`$$\newcommand{\dmacs}{d_\mathrm{MACS}}$$`
`$$\newcommand{\bv}[1]{\boldsymbol{\mathbf{#1}}}$$`

# Overview

### What is measurement invariance?

### An attempt to synthesize invariance studies on a depression scale across genders (G. Zhang, Yue, & Lai)

### Effect size for noninvariance

### Practical invariance at the test score level

- Region of measurement equivalence (Y. Zhang, Lai, & Palardy)

- Impact on selection/diagnostic/classification accuracy (Lai & Y. Zhang)

???

- Background
    * Graph of measurement invariance
        * Numerical representation
        * Weighting scale in the moon vs. the earth
    * A lot of invariance studies
        * Problem: Are invariance results interpretable?
        * Problem: How do we make use of invariance results?
    * Example: CES-D
        * All items were found noninvariant in at least one study
        * Studies generally do not reference earlier study on same/similar research questions
        * Very little consequences for subsequent practices
            
            * Most papers still uses the same CES-D score for regression analyses



- Adjusted estimations and inferences
    * Using traditional SEM framework
        * Also cite alignment papers
        * CONS: A complex model for a simple research question
        * CONS: Interpretational confounds/propagation of errors
            * Use examples from Levy (2017)
        * CONS: 
    * Using two-step approaches
        * Integrative data analysis
            * Does not incorporate measurement error in factor scores
        * Factor score regression (not yet studied for invariance)
    * Two-Stage Path Analysis
        * Step 1: factor score estimation, with reliability information
            * CFA, IRT, network quantities, as long as 
            information on reliability is available
        * Step 2: path analysis with definition variables
            * Reliability adjustment (much earlier in the literature)
            * But, individual-specific reliability is allowed, using 
            definition variables
            * Can be done in OpenMx and Mplus, and potentially in Bayesian
            engines (not sure in `blavaan`)
            * Does require normality assumption on the conditional sampling/posterior
            distributions of the factor scores
                * May not hold for IRT models in small samples
      * Simulation results

---

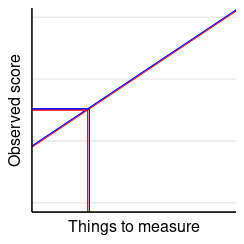
# Measurement Invariance

That the same construct is measured in the same way

]

Examples

- Same distance, same number in different states

* cf. kilometer vs. mile

- Blood pressure not systematically higher or lower

* cf. blood pressure machine in grocery vs. in hospital

]

---

# Psychological Measurement

![](images/rule2.png)

---

# With Measurement Error

???

Instead of requiring the same score, it requires the same probability distribution

---

# Formal Definition (Mellenbergh, 1989)

- For `$y_j$`, the score of the `$j$`th item, 
`$$P(y_j | \eta, G = g) = P(y_j | \eta) \quad \text{for all } g, \eta$$`

---

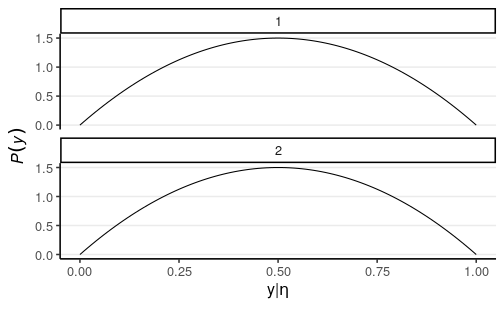
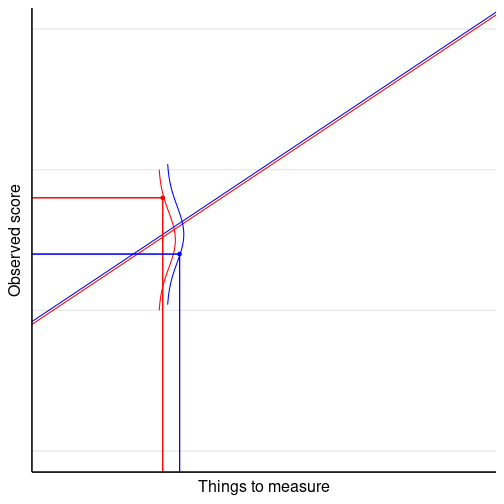
# Violation of Measurement Invariance (aka Non-Invariance)

E.g.,

- `$\eta$` = true depression level
- `$y$` = scores on the Center for Epidemiologic Studies Depression Scale (CES-D)

]

]

---

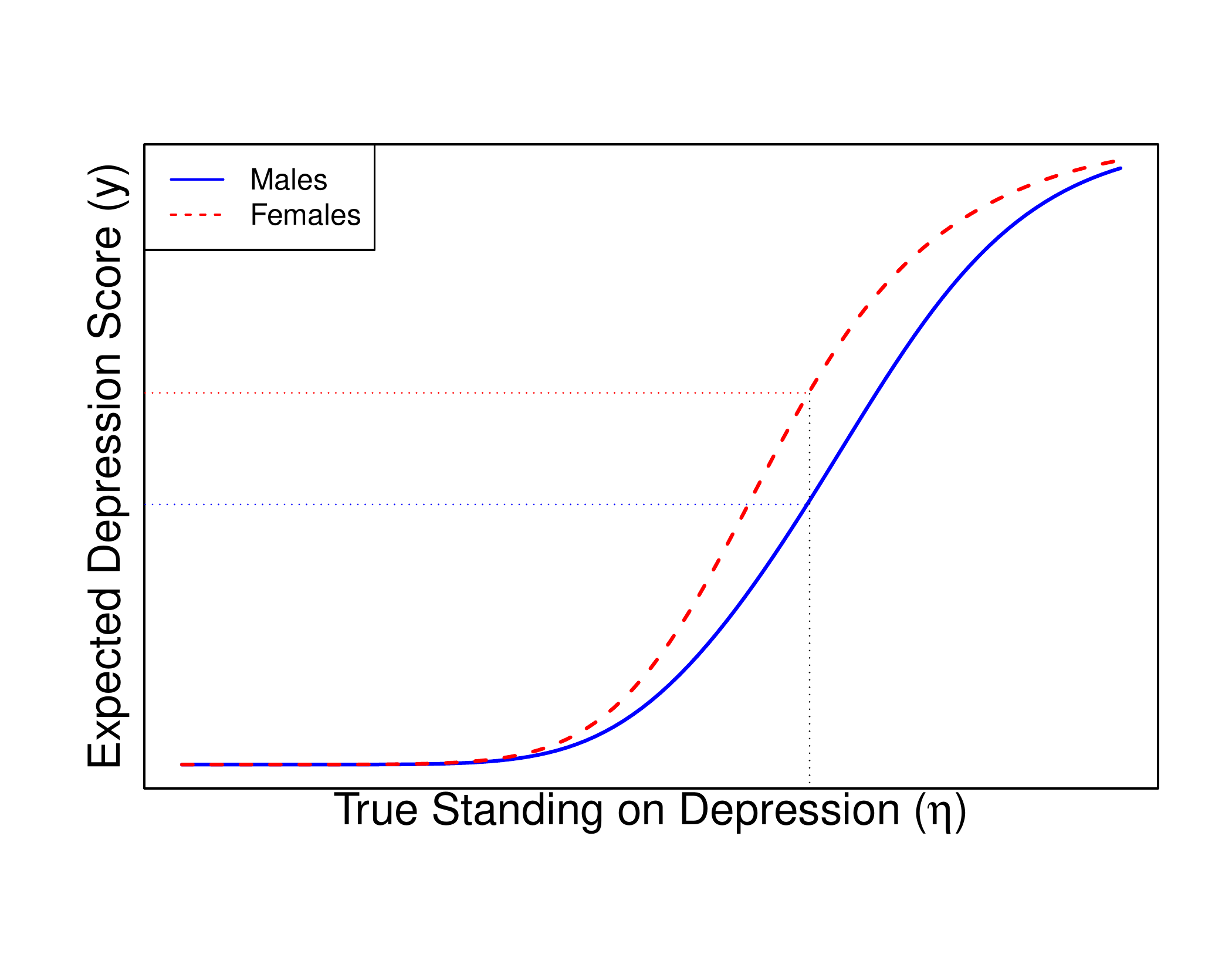
# Invariance Research Is Popular

PsycINFO Keyword (2000 Jan 1 to 2020 Dec 31): 
```
ti("measurement invariance" OR "measurement equivalence" OR 
"factorial invariance" OR "differential item functioning") OR 
ab("measurement invariance" OR "measurement equivalence" OR 
"factorial invariance" OR "differential item functioning")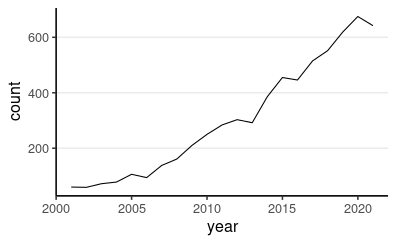
```

---

# What Should We Do When Invariance Does Not Hold?

For subsequent analyses

- Use latent variable models with partial invariance

- Or factor scores (e.g., McNeish & Wolf, 2020; Curran et al., 2009)

* Though most researchers still use composite scores

---

# Can We Still Use the Test in the Future?

### Discard the Test?

### Delete noninvariant items?

### Should it depend on the size of noninvariance?

--

### Does invariance generally hold in psychological measurement?

### Or even in physical measurement?

- Could two thermostats of the same model show a systematic difference of 0.01 degree? 0.0001 degree?

---

# Can the Invariance Hypothesis Be True in Practice?

Nil hypothesis (Cohen, 1994)

- `$H_0$`: `$\boldsymbol{\omega} = 0$` 
    * I.e., absolutely zero difference in measurement parameters across groups

"My work in power analysis led me to realize that the nil hypothesis is always false." (p. 1000)

---
class: inverse, center, middle

# Case Study

## CES-D Across Genders

---

# G. Zhang, Yue, & Lai (2021 IMPS presentation)

- 32 articles conducting invariance tests on CES-D across genders

![](images/cesd_invariance.png)

---

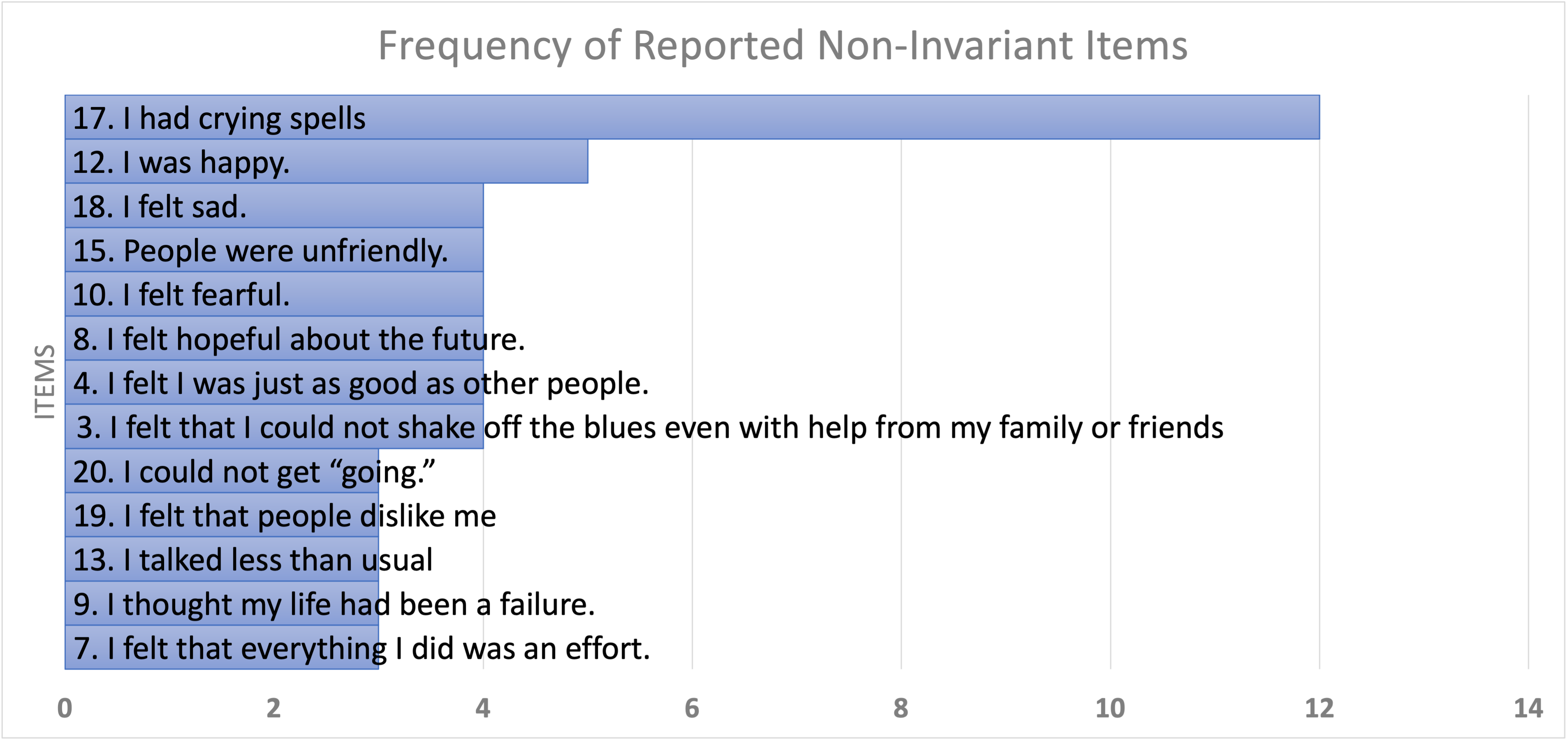
### EVERY ONE of the 20 CES-D items was found noninvariant at least once

Possible reasons

- False positives

- Inconsistent methods and cutoffs used to determine invariance

- Gender is confounded with some other sample characteristics that differ across studies

- Or, the invariance hypothesis is always rejected when sample size is large

---

# Case Study: CES-D Across Genders

Generally, each study gives binary results on invariance/noninvariance

- Hard to summarize/synthesize the invariance literature

- Practical implications?

* Dropping the "crying spell" item?
    * Different cutoffs for screening?
    
???

Like repeating the history in early studies when each study is either significant/non-significant

---

# Effect Size

- Meade (2010) "A taxonomy of effect size measures"

- Nye & Drasgow (2011): more comparable to the popular Cohen's `$d$`

`$${\dmacs}_j$$`
`$$= \frac{1}{\mathit{SD}_{jp}} \sqrt{\int \mathrm{E}(Y_{jR} - Y_{jF} | \eta)^2 f_F(\eta) d \eta}$$`
(*F* = focal group, *R* = reference group)

- Extensions in Nye et al. (2019) and Gunn et al. (2020) on signed differences

]

]

???

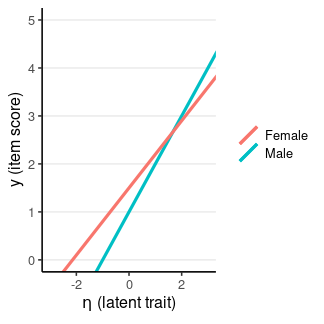
How much does the noninvariance lead to group differences in the item scores in standardized unit

---

# Effect Sizes in the CES-D Invariance Synthesis

- Only 31% provided sufficient information to compute `$\dmacs$`

* For ones that can be computed, `${\dmacs}_\text{female - male}$` = -.20 to .97
    
--

- Information commonly missing: loadings, intercepts, item SDs

---

# Summary

- Invariance results are highly inconsistent across studies (at least for binary conclusions)

- Little synthesis across invariance studies

- Implication for future use of the test is unclear

## Recommendations

- Compute effect sizes in invariance studies
    * Need software implementation
    
- Report group-specific parameters, or sufficient statistics (e.g., means and covariance matrix)

---

---
class: inverse, center, middle

# (Practical) Invariance at the Test Score Level

---

# Why Test Scores?

Usually, test scores, not item scores, are used for

- Operationalization of constructs in research

- Comparing individuals on psychological constructs

- Making selection/diagnostic/classification decisions

Noninvariance in items may cancel out

### Test invariance/lack of differential test functioning

`$$P(T | \eta, G = g) = P(T | \eta) \quad \text{for all } g, \eta$$`

---

# Y. Zhang, Lai, & Palardy (Under Review)

### When can we say a test is practically invariant with respect to `$G$`?

### A Bayesian region of measurement equivalence (ROME) approach

---

# Example

Educational Longitudinal Study (ELS: 2002; U.S. Department of Education, 2004)

- *N* = 11,663 10th grade students (47.69% male, 52.31% female)

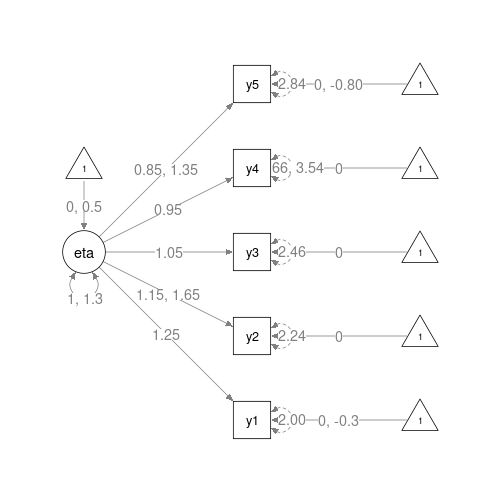
5-Item Math-Specific Self-Efficacy  
(1 = *Almost Never* to 4 = *Almost Always*)

1. I'm certain I can understand the most difficult material presented in my math texts.
2. I'm confident I can understand the most complex material presented by my math teacher.
3. I'm confident I can do an excellent job on my math assignments.
4. I'm confident I can do an excellent job on my math tests. 
5. I'm certain I can master the skills being taught in my math class.

---

![](images/zhang&lai_table2.png)

`$\dmacs$` = 0.097 to 0.11 for items 2, 4, 5

Test level: `$d = \frac{1}{\mathit{SD}_{Tp}} \sqrt{\int \mathrm{E}(T_{R} - T_{F} | \eta)^2 f_F(\eta) d \eta} = .026$`

???

Limitation: overall ES may be small, but the test may not be suitable for specific population

---

# Can We Conclude the Scale is Practically Invariant?

Null hypothesis significance testing does not allow accepting the null hypothesis (e.g., Yuan & Chan, 2016)

- `$H_0$`: `$\Delta \boldsymbol{\omega} = \mathbf{0}$`
    * `$\boldsymbol{\omega}$`: measurement parameters

- Equivalence testing by Yuan & Chan (2016)
    * Rely on a fit index (e.g., RMSEA) metric

---

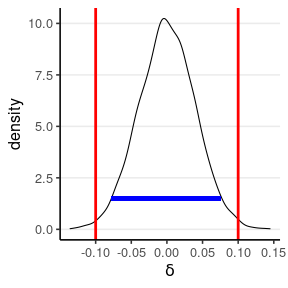
# Region of Practical Equivalence (ROPE)

Accept `$\delta = 0$` practically if `$P(\delta \in \text{ROPE})$` is high

- `$\delta$`: some measure of difference between groups

- ROPE (Berger & Hsu, 1996; Kruschke, 2011): 
    * values inside `$[\delta_{0L}, \delta_{0U}]$` considered practically equivalent to null
    
    * Reject `$H_0$`: `$|\delta| \geq \epsilon$` for some small `$\epsilon$` when 
    
        * highest posterior density interval (HPDI) is completely within ROPE

???

E.g., pharmaceutical industry, whether two drugs are equivalent to make the drug generic; bioequivalence

---

# Region of Practical Equivalence (ROPE)

Accept `$\delta = 0$` practically if `$P(\delta \in \text{ROPE})$` is high

- `$\delta$`: some measure of difference between groups

- ROPE (Berger & Hsu, 1996; Kruschke, 2011): 
    * values inside `$[\delta_{0L}, \delta_{0U}]$` considered practically equivalent to null
    * Reject `$H_0$`: `$|\delta| \geq \epsilon$` for some small `$\epsilon$` when 
        * highest posterior density interval (HPDI) is completely within ROPE
        
]

]

---

# Our Proposal: Region of Measurement Equivalence (ROME)

- `$\delta = \mathrm{E}(T_2 - T_1 | \eta) = (\sum_j \Delta \nu_j) + (\sum_j \Delta \lambda_j) \eta$`

- Determining ROME
    * Requires substantive judgment
    * Kruschke (2011) recommended half of small effect size: `$[-0.1 s_{Tp}, 0.1 s_{Tp}]$`

- Options we considered
    * 2.5% of total test score range (5 to 20)
        * or `$[-0.375, 0.375]$`
    * 0.1 `$\times$` pooled *SD* of total score
        * or `$[-0.412, 0.412]$`

---

# Using ROME

- Practically invariant if HPDI of `$E(T_2 - T_1 | \eta)$` is within ROME for all practical levels of `$\eta$`

- If not, can identify whether the test is practically invariant for some levels of `$\eta$`

---

# Test Characteristic Curve

Estimation with *blavaan* (Merkle et al.)

![](images/zhang&lai_fig2.png)

---

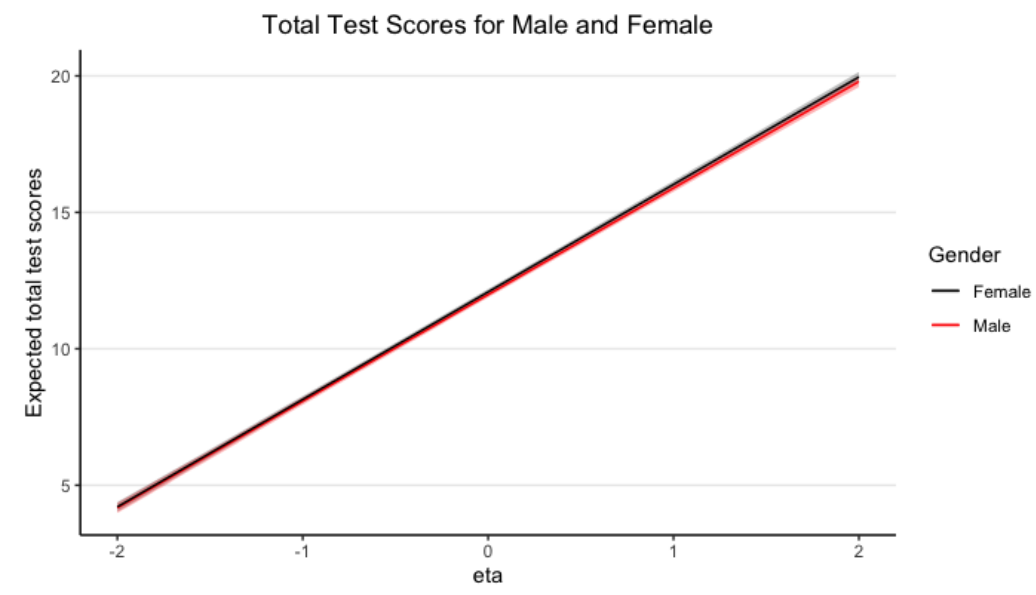
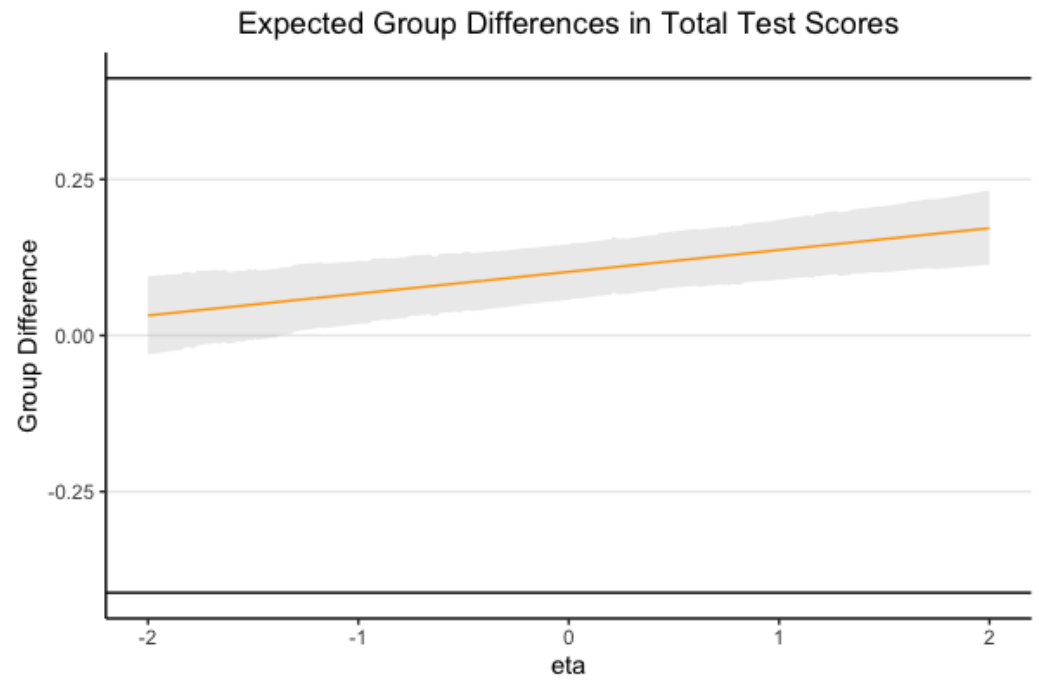
# Expected Group Differences (Female - Male)

Black horizontal lines indicate ROME

![](images/zhang&lai_fig3.png)

---

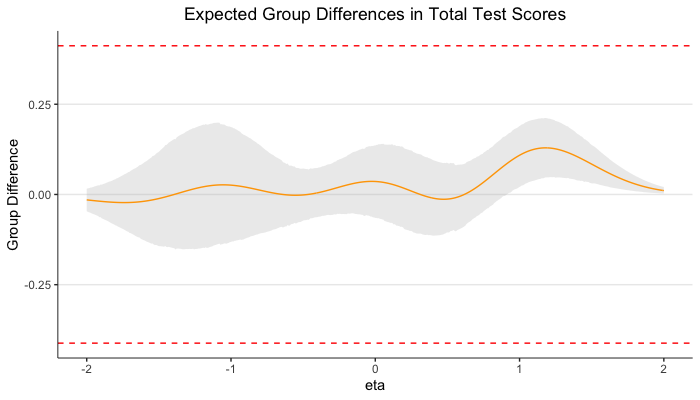
# Ordinal Factor Analysis

Estimation with Mplus (`ESTIMATOR=BAYES`)

![](images/zhang&lai_figs3.png)

---
class: inverse, middle, center

# Selection/Diagnostic/Classification Accuracy

---

# How Does Noninvariance Impact Selection Accuracy?

Tests are commonly used to make binary decisions

![](images/sai_eq.png)

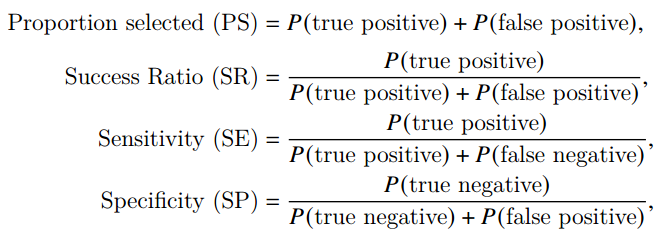
`$$\text{Adverse Impact (AI) ratio} = \frac{\mathrm{E}_R(\text{PS}_F)}{\text{PS}_R},$$`

]

]

???

SR is also called positive predictive value

---

# Classification Accuracy Indices

Millsap & Kwok (2004); Stark et al. (2004)

- Does noninvariance affect classification accuracy?

![](images/lai&zhang_fig2.png)

---

![](images/ucaa_ex.png)

Shiny App: https://partinvmmm.shinyapps.io/partinvshinyui/

---
exclude: true

# Extensions

- Lai et al. (2017): R script
- Lai et al. (2019): Binary items
- Gonzalez & Pelham (2021): Ordinal items
- Gonzalez et al. (2021): Classification consistency

---

# Lai & Y. Zhang (accepted)

### Multidimensional Classification Accuracy Analysis (MCAA)

When selection based on multiple subtests

E.g., 20-item mini-IPIP (International Personality Item Pool)

Agreeableness, Conscientiousness, Extraversion, Neuroticism, Openness to Experience

- Sample (Ock et al., 2020)
    * N = 564 (239 males, 325 females; 97.7% Caucasian)

- Four items with noninvariant intercepts, three items with noninvariant uniqueness

---

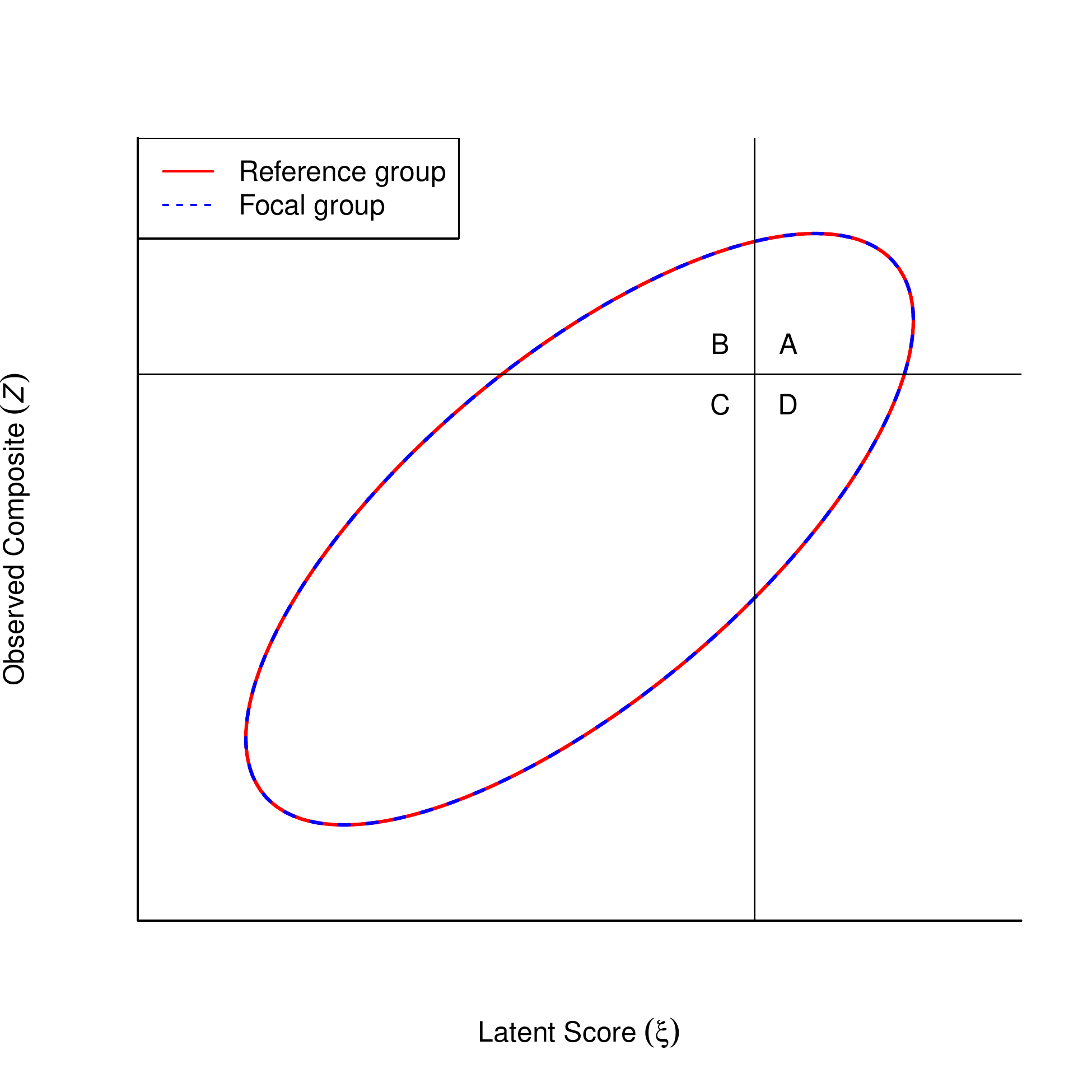
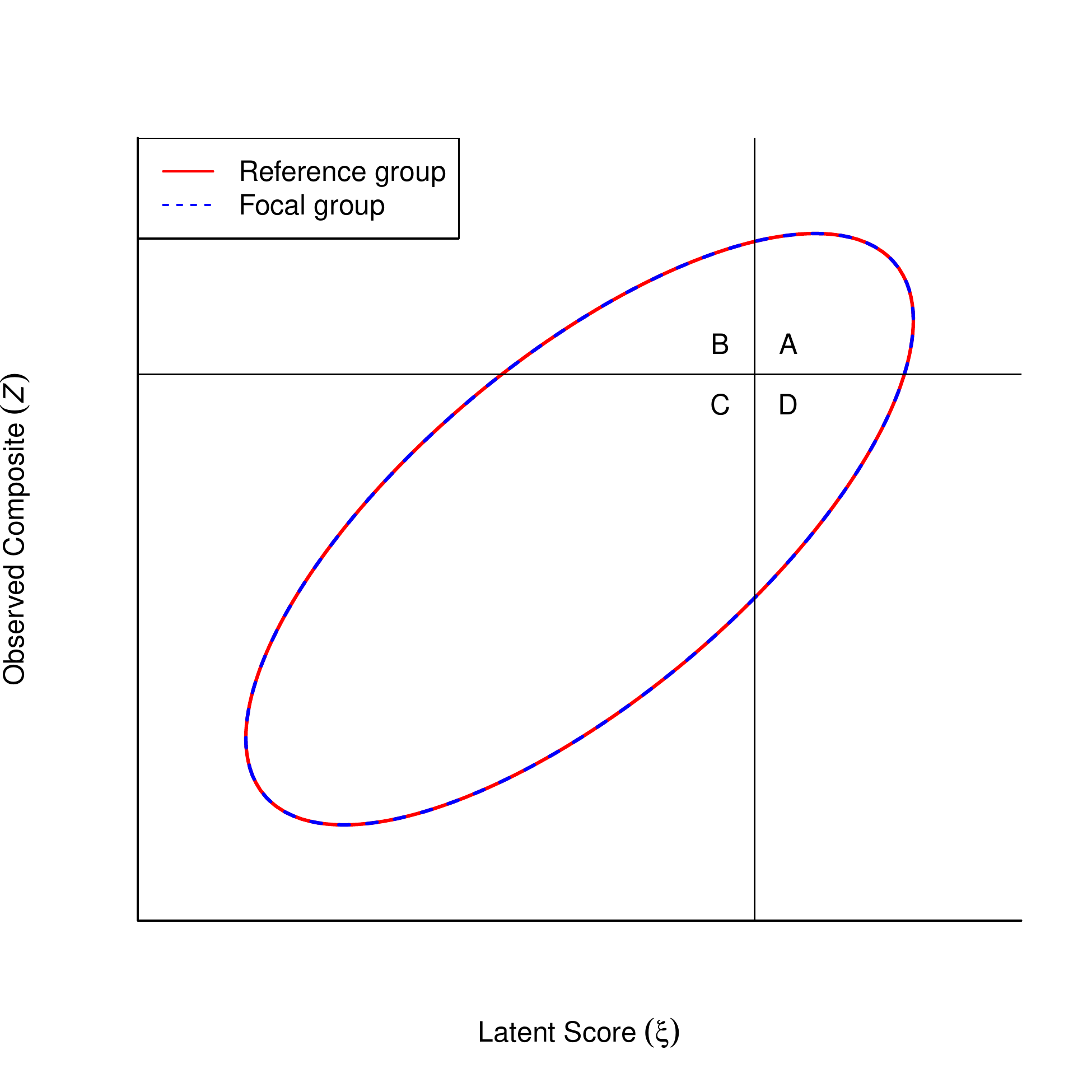
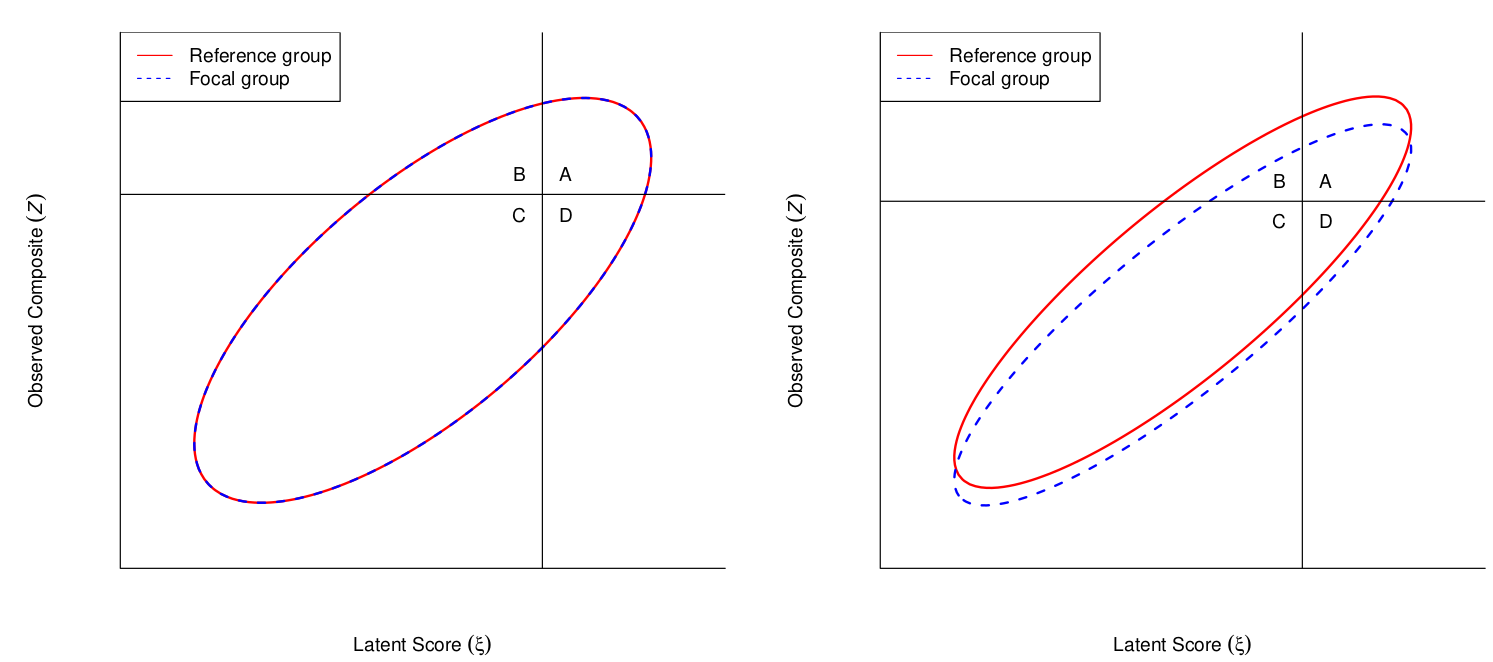
Latent composite: `$\zeta = \mathbf{w} \boldsymbol{\eta}$`

Observed composite: `$Z = \mathbf{c} \mathbf{y}$`

`\begin{equation}
  \begin{pmatrix}
   Z_g \\
   \zeta_g \\
\end{pmatrix} = N\left(\begin{bmatrix}
                          \bv c \bv \nu_g +  \bv c \bv \Lambda_g \bv \alpha_g \\
                          \bv w \bv \alpha_g
                       \end{bmatrix},
                       \begin{bmatrix}
                          \bv c \bv \Lambda_g \bv \Psi_g \bv \Lambda'_g \bv c' + 
                            \bv c \bv \Theta_g \bv c'  & \\
                          \bv c \bv \Lambda_g \bv \Psi_g \bv w' & \bv w \bv \Psi_g \bv w' 
                        \end{bmatrix} \right)
\end{equation}`

---

Selection weights based on previous studies on criterion validity of the mini-IPIP

![](images/lai&zhang_weights.png)

---

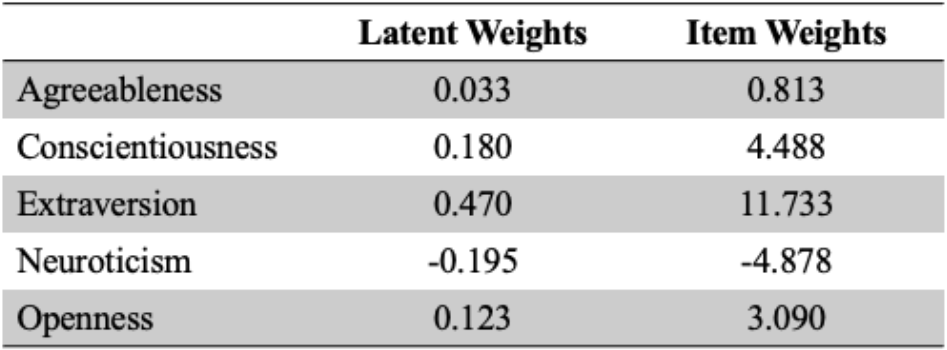
When using the mini-IPIP to select the top 10% of candidates . . .

![](images/lai&zhang_tab3.png)

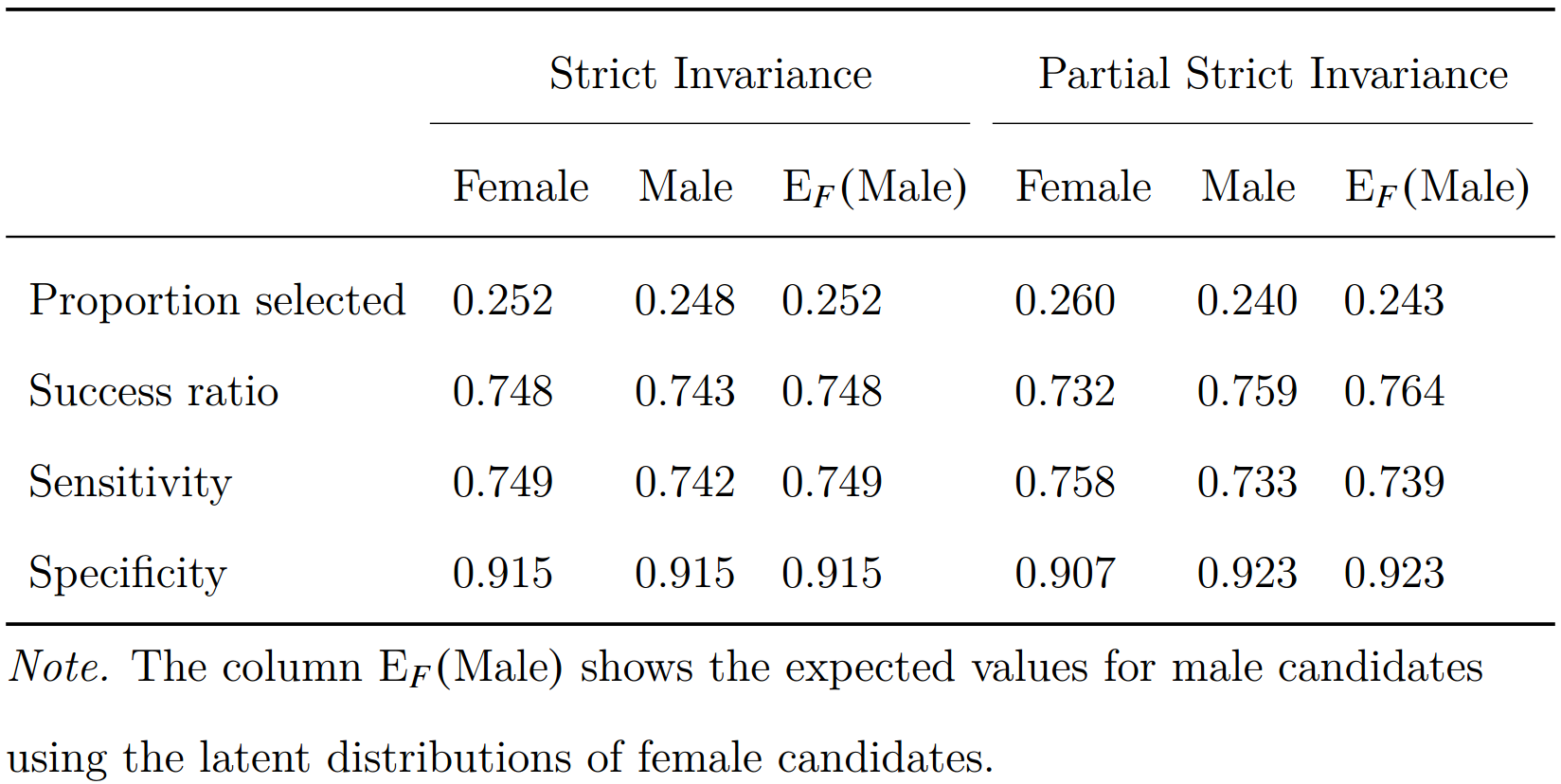
AI ratio = 0.93: slight disadvantage for males due to noninvariance

---

# Summary

Despite tremendous growth in invariance research, the practical implications of empirical studies are unclear

In my opinions, reporting measures of practical significance is a step forward for understanding how noninvariance

- affects item/test scores
- affects classification accuracy, prevalence, selection ratio, etc

Measures of practical significance can be used to set thresholds for practical invariance

- Region of measurement equivalence (ROME)

More research efforts needed to translate and synthesize invariance research

---

# Future Research

- Synthesizing effect sizes from invariance research
    
    * Need sampling variability of `$\dmacs$`
    
--

- ROME with alignment/Bayesian approximate invariance
    * Bypass the need to find a partial invariance model

- Uncertainty bounds for classification accuracy

---

# References

Berger, R. L., & Hsu, J. C. (1996). Bioequivalence trials, intersection-union tests and equivalence confidence sets. Statistical Science, 11(4), 283–319. https://doi.org/10.1214/ss/1032280304

Cohen, J. (1994). The earth is round (p < .05). American Psychologist, 49(12), 997–1003. https://doi.org/10.1037/0003-066X.49.12.997

Curran, P. J., & Hussong, A. M. (2009). Integrative data analysis: The simultaneous analysis of multiple data sets. Psychological Methods, 14(2), 81–100. https://doi.org/10.1037/a0015914

Gunn, H. J., Grimm, K. J., & Edwards, M. C. (2020). Evaluation of six effect size measures of measurement non-Invariance for continuous outcomes. Structural Equation Modeling: A Multidisciplinary Journal, 27(4), 503–514. https://doi.org/10.1080/10705511.2019.1689507

Kruschke, J. (2011). Bayesian assessment of null values via parameter estimation and model comparison. Perspectives on Psychological Science, 6(3), 299–312. https://doi.org/10.1177/1745691611406925

McNeish, D., Wolf, M.G. Thinking twice about sum scores. Behav Res 52, 2287–2305 (2020). https://doi.org/10.3758/s13428-020-01398-0

---

# References (cont'd)

Meade, A. (2010). A taxonomy of effect size measures for the differential functioning of items and scales. Journal of Applied Psychology, 95(4), 728–743. https://doi.org/10.1037/a0018966

Mellenbergh, G. J. (1989). Item bias and item response theory. International Journal of Educational Research, 13(2), 127–143. https://doi.org/10.1016/0883-0355(89)90002-5

Millsap, R. E., & Kwok, O.-M. (2004). Evaluating the impact of partial factorial invariance on selection in two populations. Psychological Methods, 9(1), 93–115. https://doi.org/10.1037/1082-989X.9.1.93

Nye, C. D., Bradburn, J., Olenick, J., Bialko, C., & Drasgow, F. (2019). How big are my effects? Examining the magnitude of effect sizes in studies of measurement equivalence. Organizational Research Methods, 22(3), 678–709. https://doi.org/10.1177/1094428118761122

Nye, C. D., & Drasgow, F. (2011). Effect size indices for analyses of measurement equivalence: Understanding the practical importance of differences between groups. Journal of Applied Psychology, 96(5), 966–980. https://doi.org/10.1037/a0022955

---

# References (cont'd)

Stark, S., Chernyshenko, O. S., & Drasgow, F. (2004). Examining the effects of differential item (functioning and differential) test functioning on selection decisions: When are statistically significant effects practically important? Journal of Applied Psychology, 89(3), 497–508. https://doi.org/10.1037/0021-9010.89.3.497

U.S. Department of Education, National Center for Education Statistics. (2004). Education longitudinal study of 2002: Base year data file user’s manual, by Steven J. Ingels, Daniel J. Pratt, James E. Rogers, Peter H. Siegel, and Ellen S. Stutts. Washington, DC.

Yuan, K. H., & Chan, W. (2016). Measurement invariance via multigroup SEM: Issues and solutions with chi-square-difference tests. Psychological Methods, 21(3),405–426. https://doi.org/10.1037/met0000080

---

# Thanks!

Questions?

My email: hokchiol@usc.edu

Slides created via the R package [**xaringan**](https://github.com/yihui/xaringan).

The chakra comes from [remark.js](https://remarkjs.com), [**knitr**](https://yihui.org/knitr/), and [R Markdown](https://rmarkdown.rstudio.com).