class: center, middle, inverse, title-slide # Multilevel Bootstrap Confidence Intervals for Standardized Effect Size ### Hok Chio (Mark) Lai ### University of Southern California ### 2020/07/14 --- # Overview ### Multilevel Bootstrap ### The "bootmlm" package ### Effect size for cluster-randomized trials ### Simulation Results Lai, M. H. C. (2020). Bootstrap confidence interval for multilevel standardized effect size. *Multivariate Behavioral Research*. 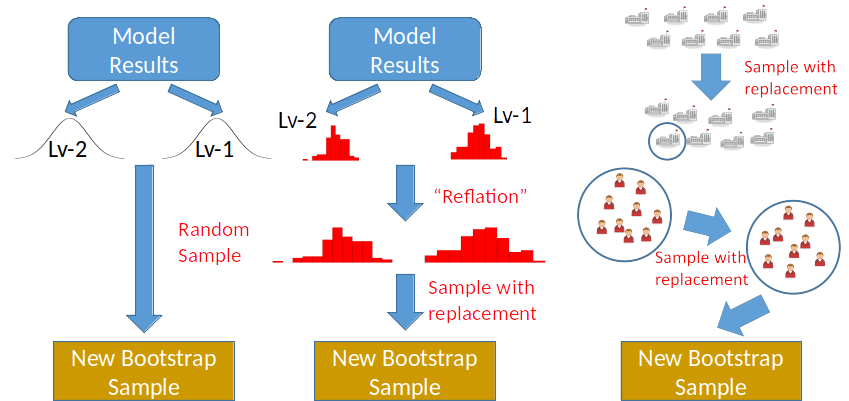https://doi.org/10.1080/00273171.2020.1746902 --- # Multilevel Bootstrap Confidence Interval (CI) Good alternatives to analytic CIs - for quantities with nonnormal sampling distributions - when analytic CIs are hard to obtain - when some model assumptions are violated --- # Parameteric, Residual, and Case Bootstrap  ??? - Parametric: no normal sampling distribution assumption - Residual: no multivariate normality assumption on error terms - Case: no parametric assumptions --- # Types of Bootstrap CIs Received less attention in the multilevel literature - Normal: `\([\hat \theta \pm 2 \sqrt{v^*}]\)` - Basic/percentile-*t*: `\([2 \hat \theta - \hat \theta^*_{1 - \alpha / 2}, 2 \hat \theta - \hat \theta^*_{\alpha / 2}]\)` - Studentized/Bootstrap-*t*: `\((\hat \theta - \theta) / \sqrt{v}\)` as pivot - Percentile: `\([\hat \theta^*_{\alpha / 2}, \hat \theta^*_{1 - \alpha / 2}]\)` - Bias-corrected and accelerated (BCa): correct for bias and skewness (acceleration) --- class: inverse, middle, center # R Package `bootmlm` --- # `bootmlm` https://github.com/marklhc/bootmlm - Implement various bootstrapping schemes and bootstrap CIs - Additional experimental functionality * e.g., weighted bootstrap based on sampling weights (Wen & Lai, under reviewer) - Currently only supports `lme4::lmer()` in R --- # Example ```r fm01ML <- lmer(Yield ~ (1 | Batch), Dyestuff, REML = FALSE) mySumm <- function(x) { # Function to extract fixed effects and level-1 error SD c(getME(x, "beta"), sigma(x)) } # Covariance preserving residual bootstrap boo01 <- bootstrap_mer(fm01ML, mySumm, type = "residual", nsim = 100) # Get confidence interval boot.ci(boo01, index = 2, type = c("norm", "basic", "perc")) # BCa using influence values computed from `empinf_mer` boot.ci(boo01, index = 2, type = "bca", L = empinf_mer(fm01ML, mySumm, 2)) ``` --- class: inverse, middle, center # Multilevel Effect Size --- # Cluster-Randomized Trials (CRTs)  ??? Image credit: [Wikimedia Commons](https://commons.wikimedia.org/wiki/File:Sharingan_triple.svg) --- # Motivating Example ## Haug et al. (2017) - Outcome: Estimated peak blood alcohol concentration (BAC) .pull-left[ ### Intervention - Web- and text messaging-based intervention - `\(N^T = 547\)` students from `\(J^T = 43\)` schools ] .pull-right[ ### Control - Assessment only - `\(N^C = 494\)` students from `\(J^T = 37\)` schools ] --- # Multilevel Effect Size - Estimated treatment effect (from simulated data) = -0.09, *SE* = 0.09 * Need to interpret the magnitude of the effect ### Extension of Cohen's `\(d\)`/Hedges's `\(g\)` - Hedges (2007, p. 348), using summary statistics `$$d = \frac{\bar Y^T_{..} - \bar Y^C_{..}}{\hat \sigma_\text{Total}}$$` - Hedges (2009, 18.24), using linear-mixed-effect model estimates `$$\hat \delta = \frac{\hat \gamma}{\sqrt{\hat \sigma^2_W + \hat \sigma^2_B}}$$` --- # Analytic Approximate CIs Available, But - Sampling distribution of effect size is generally not normal - Random effects/error terms may be non-normal * For BAC, skewness ~ 2, kurtosis ~ 4.8 - Not scalable to more complex designs * Hedges (2011) for 3-level; Lai & Kwok (2014) for cross-classified; Lai & Kwok (2016) for partially nested designs --- # Using `bootmlm` ``` d d_boot normal.ll normal.ul basic.ll basic.ul -0.092 -0.092 -0.278 0.095 -0.274 0.097 student.ll student.ul percent.ll percent.ul bca.ll bca.ul -0.281 0.097 -0.281 0.089 -0.263 0.119 ``` ### Compared to Ignoring the clustered structure: *d* = -0.92, 95% CI [-0.207, 0.036] - CI width about 35% too short --- class: inverse, center, middle # Monte Carlo Simulation Study --- # Design Conditions |Factor |Levels | |:--------------------------|:------------------| |ICC |.05, .10, .20 | |Level-2 skew |Normal, skewed | |Level-1 skew |Normal, skewed | |# Clusters (*J*) |20, 30, 70 | |Average cluster size (*n*) |5, 25 | |Imbalance |Balance, imbalance | |Population Effect Size |0, 0.5 | ### Data Generating Model `$$y_{ij} = \gamma_{00} + \gamma_{01} \text{TREAT}_j + u_{0j}$$` Case bootstrap did not perform well, consistent with previous literature --- 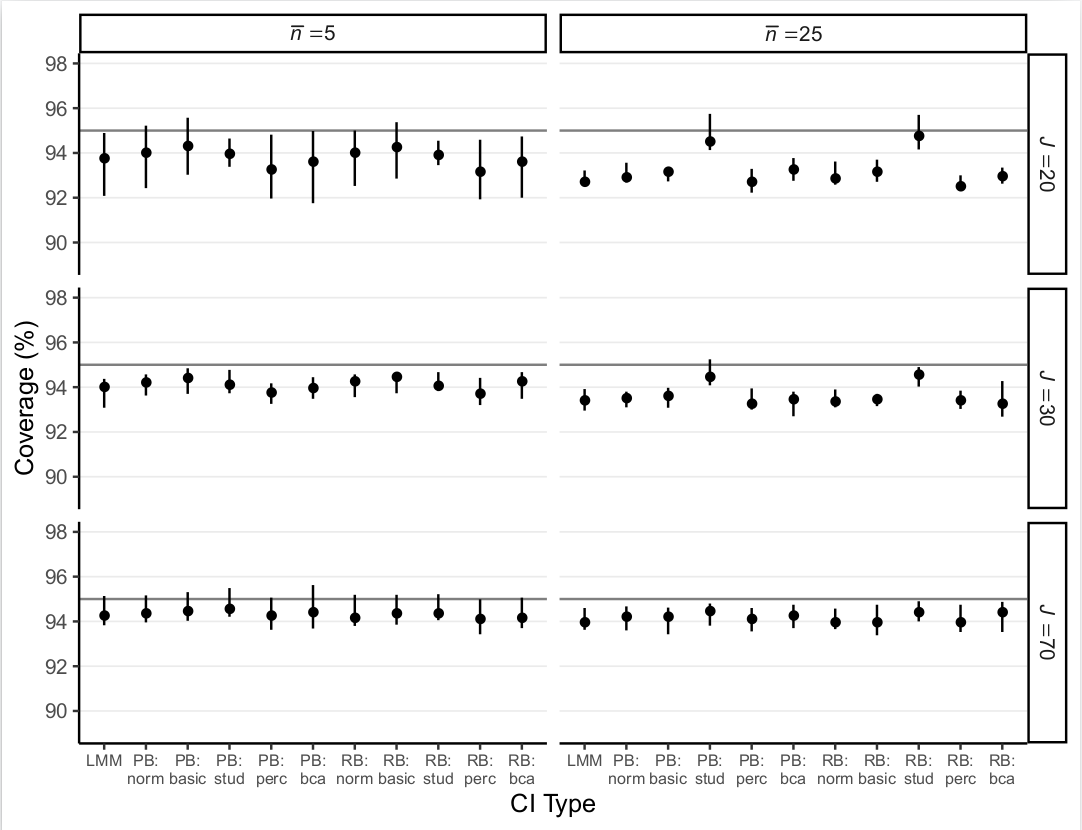Normal Data  --- 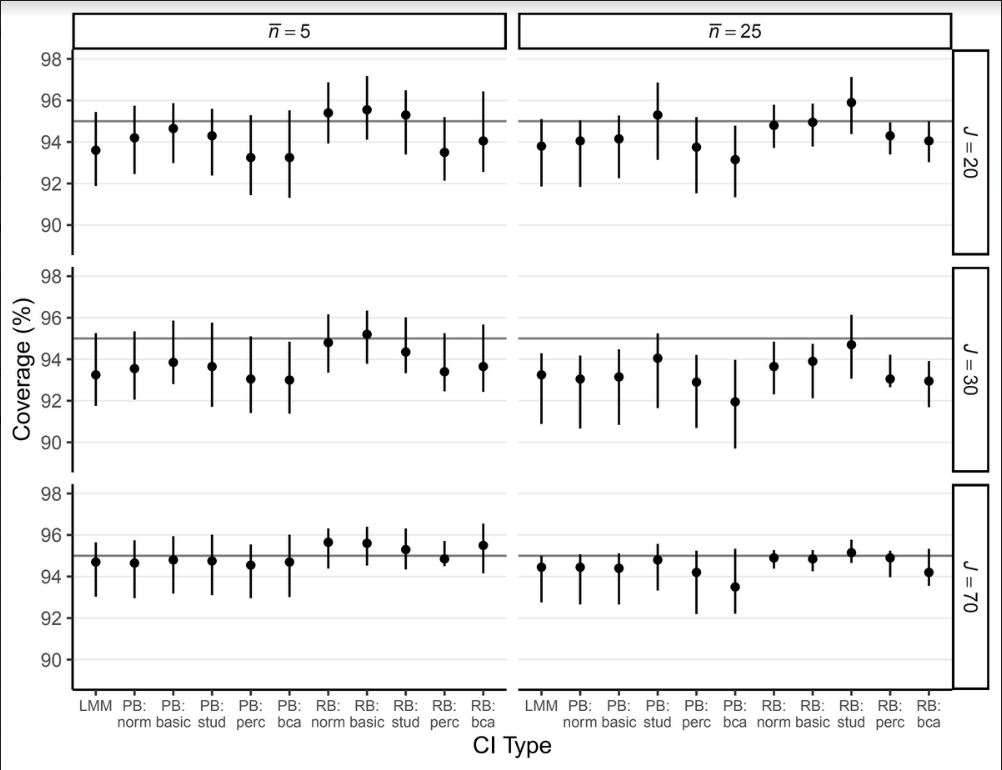Skewed at Both Levels  --- # Summary of Results .pull-left[  ] .pull-right[ - Residual bootstrap with studentized CI performed best overall - Residual bootstrap with basic CI performed best in small samples - Effect of nonnormality is modest on coverage rates ] --- # Conclusions - Bootstrap CIs can be obtained when analytic CIs are hard to obtain - Residual bootstrap with studentized/basic CIs are promising for effect size ### Future work is needed - Other designs (crossed, covariate-adjusted, etc) - Other quantities (e.g., `\(R^2\)`, indirect effects) --- class: center, middle # Thanks! For questions, email me at [hokchiol@usc.edu](mailto:hokchiol@usc.edu) For full results, see the [full paper](https://doi.org/10.1080/00273171.2020.1746902) Slides created via the R package [**xaringan**](https://github.com/yihui/xaringan).