+ - 0:00:00
Notes for current slide
Notes for next slide

Ask them to introduce themselves and what research they are interested in

Like a lot of terminologies in statistics

Multilevel Modeling (MLM)

An Introduction

Mark Lai

2018/11/27

1 / 50

Different Names

Hierarchical linear model (HLM; Raudenbush and Bryk, 2002)

Mixed/Mixed-effects model (Littell, Milliken, Stroup, et al., 1996)

Random coefficient model (de Leeuw and Kreft, 1986)

Variance component model (Aitkin and Longford, 1986)

2 / 50

Ask them to introduce themselves and what research they are interested in

Like a lot of terminologies in statistics

Roadmap

What are multilevel data?

Why use MLM?

  • Avoid underestimated SE
  • Research questions at different levels
  • Cluster-specific (or person-specific) regression lines
3 / 50

Multilevel Data

Nested Data

  • Students in classrooms/schools
  • Siblings in families
  • Clients in therapy groups/therapists/clinics
  • Employees in organizations in countries

4 / 50

What other examples can you think about?

Multilevel Data

  • Repeated measures in individuals

Network Graph

boxes_and_circles A A 1 1 A->1 2 2 A->2 3 3 A->3 B B 4 4 B->4 5 5 B->5 C C 6 6 C->6 7 7 C->7 8 8 C->8 9 9 C->9 D D 10 10 D->10 11 11 D->11
5 / 50

Nesting: multiple units belongs to the same higher-level unit Level-1: lowest level; Level-2: the next level

Applications of MLM

Psychotherapy

  • Heterogeneity of treatment effectiveness across therapists

Educational research

  • teacher expectations on students' performance

Organizational research

  • Job strain and ambulatory blood pressure
6 / 50

Applications of MLM (cont'd)

Cross-national/neighborhood research

  • Sociopolitical influence on psychological processes (e.g., age and generalized trust)
  • Post-materialism, locus of control, and concern for global warming

Longitudinal analysis/repeated measures

  • Aging, self-esteem, and stress appraisal
7 / 50

Example Data

Sample simulated data on students' popularity from Hox, Moerbeek, & van de Schoot (2018)

  • 2000 pupils (level 1) in 100 classrooms (level 2)
Variable Description
pupil pupil ident
class class ident
extrav extraversion
sex pupil sex
texp teacher experience in years
popular popularity sociometric score
popteach popularity teacher evaluation
8 / 50
 
9 / 50

10 / 50

Exaplain the graph, and ask for their observations

Girls are more popular; popularity related to both extraversion and teacher experience

11 / 50

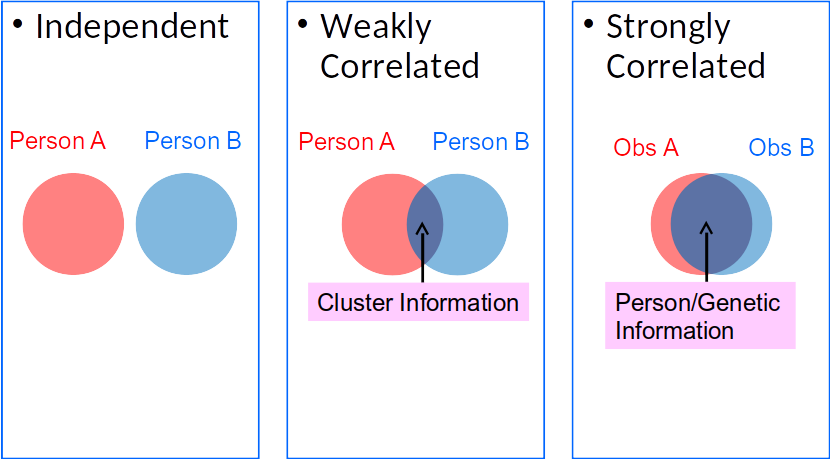
Have you learned what the independent observation assumption is? When I first learn regression, I don't really know what it means until I learn MLM

Quantify Clustering

Intraclass correlation: ICC=σ2clusterσ2cluster+σ2individual

ICC = prop. var at cluster level
= average correlation between two individuals in the same cluster

Variance components: σ2cluster, σ2individual

12 / 50

What does the formula looks like? R2

Check the variability of (a) classroom means and (b) within a classroom

ˆσ2cluster=0.702

ˆσ2individual=1.222

ICC=0.7020.702+1.222=.365

What does that mean?

13 / 50

Graph: within and between variance

36.5% variance of popular is at class level. Also, the average correlation of the popularity score of two students is .365

Dependent (Correlated) Observations

With clustered data, an assumption of OLS regression is violated

One score inform another score in the same cluster

Overlap: reduces effective information (Neff) in data

14 / 50

Two students in the same class give less than two pieces of information

Consequences

Assuming independent obs, OLS understates the uncertainty in the estimates

  • SE too small; CI too narrow

↑t=ˆβSE(ˆβ)↓

15 / 50

What's the consequence of an inflated test statistic?

Comparing OLS with MLM

## 
## Call:
## lm(formula = popular ~ texp, data = popdata)
## 
## Residuals:
## <Labelled double>: popularity sociometric score
##    Min     1Q Median     3Q    Max 
## -4.694 -0.899 -0.063  0.906  5.112 
## 
## Labels:
##  value            label
##      0  lowest possible
##     10 highest possible
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  4.20498    0.07092    59.3   <2e-16 ***
## texp         0.06110    0.00452    13.5   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.32 on 1998 degrees of freedom
## Multiple R-squared:  0.0838,    Adjusted R-squared:  0.0834 
## F-statistic:  183 on 1 and 1998 DF,  p-value: <2e-16
## Linear mixed model fit by REML ['lmerMod']
## Formula: popular ~ texp + (1 | class)
##    Data: popdata
## 
## REML criterion at convergence: 6313
## 
## Scaled residuals: 
##    Min     1Q Median     3Q    Max 
## -3.533 -0.696  0.000  0.690  3.345 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  class    (Intercept) 0.543    0.737   
##  Residual             1.222    1.105   
## Number of obs: 2000, groups:  class, 100
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)   4.1967     0.1861   22.55
## texp          0.0616     0.0118    5.21
## 
## Correlation of Fixed Effects:
##      (Intr)
## texp -0.909
16 / 50

OLS:
95% CI [0.052, 0.070].

MLM:
95% CI [0.038, 0.085].

17 / 50

Understate the uncertainty in the slopes

Type I Error Inflation

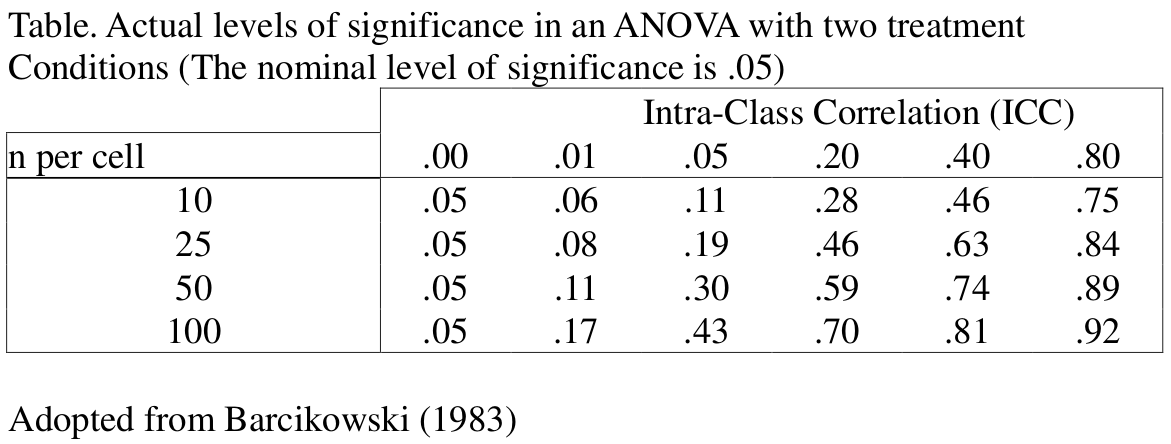
Depends on design effect: 1 + (cluster size - 1) × ICC

What's the design effect for the popularity data?

18 / 50

ICC of .20, n = 25, α inflated from .05 to .50

Give time to calculate the design effect

Lai and Kwok (2015): MLM needed when design effect > 1.1

For the popularity data, design effect
= 1 + (20 - 1) × .365 = 7.934

Neff reduces by almost 8 times: 2000 → 252

19 / 50

Random Coefficient Model

For lv-2 predictor, OLS generally results in underestimated SE

For lv-1 predictor, in addition to problem on SE, OLS result does not show heterogeneity across groups

20 / 50

OLS With All Data

Consider extrav --> popular (with extrav mean centered)

21 / 50

Think About Just One Classroom

populari=β0+β1extravi+ei

22 / 50

Ask them to point out where β0, β1, and ei are

Think About Just One Classroom

populari1=β01+β11extravi1+ei1

23 / 50

Think About Classroom 35

populari35=β035+β135extravi35+ei35

24 / 50

Classroom 14

populari14=β014+β114extravi14+ei14

25 / 50

OLS Lines for 100 Classrooms + Average Line

popularij=β0j+β1jextravij+eij

26 / 50

Partial Pooling

For each classroom, n=10 for OLS

For average line, N=1,000

MLM with partial pooling: weighted average of the OLS line and the average line

  • Borrowing information from other clusters
27 / 50

Which one should you trust more?

Get more stable estimates of regression lines

OLS

MLM

28 / 50

What's the difference in the individual slopes across the two graphs?

β0j and β1j assumed to come from normal distributions

  • β0j∼N(γ00,σ2u0)
  • β1j∼N(γ10,σ2u1)

Fixed effects

  • γ00: average intercept
  • γ10: average slope

Random effects

  • u0j: β0j−γ00
  • u1j: β1j−γ10
29 / 50

Maybe write out the model

Fixed Effect Estimates

library(lme4)
m2s <- lmer(popular ~ extravc + (extravc | class), data = popdata)
print(summary(m2s, correlation = FALSE), show.resids = FALSE, digits = 2L)
## Linear mixed model fit by REML ['lmerMod']
## Formula: popular ~ extravc + (extravc | class)
##    Data: popdata
## 
## REML criterion at convergence: 5779
## 
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr 
##  class    (Intercept) 0.892    0.94          
##           extravc     0.026    0.16     -0.88
##  Residual             0.895    0.95          
## Number of obs: 2000, groups:  class, 100
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)    5.031      0.097      52
## extravc        0.493      0.025      19
30 / 50

Maybe do a software demo at this point

Random Effect Variance Estimates

library(lme4)
m2s <- lmer(popular ~ extravc + (extravc | class), data = popdata)
print(summary(m2s, correlation = FALSE), show.resids = FALSE, digits = 2L)
## Linear mixed model fit by REML ['lmerMod']
## Formula: popular ~ extravc + (extravc | class)
##    Data: popdata
## 
## REML criterion at convergence: 5779
## 
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr 
##  class    (Intercept) 0.892    0.94          
##           extravc     0.026    0.16     -0.88
##  Residual             0.895    0.95          
## Number of obs: 2000, groups:  class, 100
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)    5.031      0.097      52
## extravc        0.493      0.025      19
31 / 50

u0j and u1j Estimates

##     (Intercept)  extravc
## 1        0.2001 -0.02701
## 2       -0.6723  0.09697
## 3       -0.3316  0.05710
## 4        0.5640 -0.09995
## 5       -0.0822  0.02160
## 6       -0.5466  0.08376
## 7       -0.6626  0.06482
## 8       -1.2502  0.20388
## 9       -0.3227  0.07694
## 10       0.3572 -0.08819
## 11      -0.5219  0.05364
## 12      -0.3201  0.03556
## 13       1.0911 -0.16368
## 14      -2.6237  0.37981
## 15      -0.4743  0.09242
## 16      -0.4342  0.03811
## 17       0.2689 -0.02369
## 18       1.2496 -0.19917
## 19       0.6571 -0.08868
## 20       0.2252  0.00109
## 21       0.0208 -0.04727
## 22       1.2951 -0.19229
## 23       0.2055 -0.02418
## 24      -0.7570  0.11494
## 25      -0.0802 -0.01156
## 26      -0.6955  0.10710
## 27      -0.6002  0.11415
## 28      -0.3705  0.01429
## 29       1.0993 -0.18013
## 30      -0.8285  0.10970
## 31      -0.7244  0.20541
## 32      -0.0804  0.05116
## 33       1.4146 -0.13637
## 34      -0.4552  0.10145
## 35       1.9571 -0.32236
## 36       0.3317 -0.11151
## 37       0.2207 -0.01609
## 38      -0.2848  0.04430
## 39       0.2782 -0.06550
## 40      -0.6091  0.14696
## 41      -0.9680  0.12080
## 42       0.3109 -0.02819
## 43       0.3401 -0.07257
## 44      -0.2972  0.06237
## 45       0.7216 -0.12137
## 46       0.2325  0.00589
## 47      -0.0927 -0.01379
## 48      -1.1785  0.20855
## 49      -0.3443  0.05147
## 50       1.1974 -0.20811
## 51      -0.4365  0.04984
## 52      -0.5582  0.06737
## 53       1.6465 -0.23287
## 54       0.2547 -0.07409
## 55      -1.5050  0.19244
## 56      -0.1070  0.00712
## 57      -1.5458  0.24156
## 58       1.0998 -0.12649
## 59      -0.9428  0.14141
## 60      -1.5338  0.25145
## 61       0.9638 -0.12458
## 62       0.8033 -0.13504
## 63       0.3581 -0.04472
## 64       2.1316 -0.30827
## 65       1.3030 -0.22040
## 66       0.7325 -0.05845
## 67       1.4743 -0.22753
## 68       0.7837 -0.13144
## 69       0.8993 -0.14044
## 70       0.1563 -0.05321
## 71      -0.1695  0.02571
## 72       0.8337 -0.13113
## 73       0.2382 -0.01536
## 74       0.0622 -0.01092
## 75       1.7457 -0.28259
## 76      -0.2655  0.03490
## 77      -1.0844  0.18981
## 78       0.0335 -0.03235
## 79       0.0922  0.02359
## 80      -0.3891 -0.00711
## 81      -0.8835  0.13719
## 82      -2.6132  0.35655
## 83       1.0551 -0.16981
## 84       1.3292 -0.19446
## 85       1.3881 -0.23055
## 86      -1.5313  0.21197
## 87      -1.2088  0.18230
## 88      -0.2786  0.04305
## 89      -0.0727  0.03339
## 90      -0.7018  0.11680
## 91       0.0424 -0.02476
## 92      -0.4476  0.06713
## 93      -0.4874  0.08730
## 94       0.4754 -0.08232
## 95       0.0613 -0.04980
## 96       0.3719 -0.04588
## 97      -1.2084  0.21461
## 98       1.2608 -0.20162
## 99       0.0332  0.02905
## 100     -1.2887  0.22907
32 / 50

Heterogeneity in the slopes: OLS gives underestimated SE of the average slope (Lai and Kwok, 2015)

Falsely assuming constant slopes across groups

  • Heterogeneity in slopes can be an important research question
33 / 50

Cross-Level Interaction

Whether a class-level variable explains variations in class-specific slopes

34 / 50

When there is heterogeneity, the next step is to ask what can account for that

What do you observe from the graph?

Ecological Fallacy

Association between two variables can be different across levels

The third reason of using MLM

35 / 50

Class-level coefficient: ˆγ01 = 0.189, 95% CI [-0.083, 0.461]

## Inference for Stan model: stan_gpc_pv_ran_slp.
## 2 chains, each with iter=1000; warmup=500; thin=1; 
## post-warmup draws per chain=500, total post-warmup draws=1000.
## 
##                  mean se_mean    sd     2.5%      50%    97.5% n_eff Rhat
## b0               5.07    0.01  0.08     4.91     5.07     5.23   236 1.00
## b[1]             0.50    0.00  0.03     0.45     0.50     0.55   874 1.00
## bm               0.19    0.01  0.15    -0.08     0.19     0.46   195 1.00
## b_contextual    -0.31    0.01  0.15    -0.60    -0.31    -0.03   197 1.00
## sigma_y          0.95    0.00  0.01     0.92     0.95     0.97  1011 1.00
## tau_y[1]         0.87    0.01  0.07     0.75     0.87     1.03   163 1.01
## tau_y[2]         0.18    0.00  0.03     0.12     0.18     0.24   451 1.00
## sigma_x          1.09    0.00  0.02     1.06     1.09     1.12  1621 1.00
## tau_x            0.65    0.00  0.05     0.56     0.65     0.75   364 1.01
## lp__         -2205.08    1.16 16.44 -2236.88 -2205.17 -2173.03   200 1.00
## 
## Samples were drawn using NUTS(diag_e) at Sat Nov 24 22:31:54 2018.
## For each parameter, n_eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor on split chains (at 
## convergence, Rhat=1).

[1] With Bayesian estimation

36 / 50

Student-level coefficient: ˆγ10 = 0.501, 95% CI [0.45, 0.551]

## Inference for Stan model: stan_gpc_pv_ran_slp.
## 2 chains, each with iter=1000; warmup=500; thin=1; 
## post-warmup draws per chain=500, total post-warmup draws=1000.
## 
##                  mean se_mean    sd     2.5%      50%    97.5% n_eff Rhat
## b0               5.07    0.01  0.08     4.91     5.07     5.23   236 1.00
## b[1]             0.50    0.00  0.03     0.45     0.50     0.55   874 1.00
## bm               0.19    0.01  0.15    -0.08     0.19     0.46   195 1.00
## b_contextual    -0.31    0.01  0.15    -0.60    -0.31    -0.03   197 1.00
## sigma_y          0.95    0.00  0.01     0.92     0.95     0.97  1011 1.00
## tau_y[1]         0.87    0.01  0.07     0.75     0.87     1.03   163 1.01
## tau_y[2]         0.18    0.00  0.03     0.12     0.18     0.24   451 1.00
## sigma_x          1.09    0.00  0.02     1.06     1.09     1.12  1621 1.00
## tau_x            0.65    0.00  0.05     0.56     0.65     0.75   364 1.01
## lp__         -2205.08    1.16 16.44 -2236.88 -2205.17 -2173.03   200 1.00
## 
## Samples were drawn using NUTS(diag_e) at Sat Nov 24 22:31:54 2018.
## For each parameter, n_eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor on split chains (at 
## convergence, Rhat=1).

[1] With Bayesian estimation

37 / 50

Contextual effect: ˆγ01−ˆγ10 = -0.312, 95% CI [-0.598, -0.033]

## Inference for Stan model: stan_gpc_pv_ran_slp.
## 2 chains, each with iter=1000; warmup=500; thin=1; 
## post-warmup draws per chain=500, total post-warmup draws=1000.
## 
##                  mean se_mean    sd     2.5%      50%    97.5% n_eff Rhat
## b0               5.07    0.01  0.08     4.91     5.07     5.23   236 1.00
## b[1]             0.50    0.00  0.03     0.45     0.50     0.55   874 1.00
## bm               0.19    0.01  0.15    -0.08     0.19     0.46   195 1.00
## b_contextual    -0.31    0.01  0.15    -0.60    -0.31    -0.03   197 1.00
## sigma_y          0.95    0.00  0.01     0.92     0.95     0.97  1011 1.00
## tau_y[1]         0.87    0.01  0.07     0.75     0.87     1.03   163 1.01
## tau_y[2]         0.18    0.00  0.03     0.12     0.18     0.24   451 1.00
## sigma_x          1.09    0.00  0.02     1.06     1.09     1.12  1621 1.00
## tau_x            0.65    0.00  0.05     0.56     0.65     0.75   364 1.01
## lp__         -2205.08    1.16 16.44 -2236.88 -2205.17 -2173.03   200 1.00
## 
## Samples were drawn using NUTS(diag_e) at Sat Nov 24 22:31:54 2018.
## For each parameter, n_eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor on split chains (at 
## convergence, Rhat=1).

[1] With Bayesian estimation

38 / 50

Explain what a contextual effect is

Growth Curve Analysis

Individual as "cluster"

39 / 50

Find the overall trajectory and the variations around the overall trajectory

Other Forms of Clustering

Three-level

boxes_and_circles AB District 1 A A AB->A B B AB->B CD District 2 C C CD->C D D CD->D 1 1 A->1 2 2 A->2 3 3 A->3 4 4 B->4 5 5 B->5 6 6 C->6 7 7 C->7 8 8 C->8 9 9 C->9 10 10 D->10 11 11 D->11
40 / 50

Other Forms of Clustering

Cross-classification

boxes_and_circles n1 Neighborhood 1 n2 Neighborhood 2 n3 Neighborhood 3 A A 1 1 A->1 2 2 A->2 3 3 A->3 B B 4 4 B->4 5 5 B->5 C C 6 6 C->6 7 7 C->7 8 8 C->8 9 9 C->9 D D 10 10 D->10 11 11 D->11 1->n1 2->n2 3->n2 4->n1 5->n1 6->n2 7->n2 8->n3 9->n3 10->n3 11->n3

Partial Nesting

boxes_and_circles A A 1 1 A->1 2 2 A->2 3 3 A->3 B B 4 4 B->4 5 5 B->5 C C 6 6 C->6 7 7 C->7 8 8 9 9 10 10 11 11
41 / 50

Additional Resources

Chapter from Cohen, Cohen, West, et al. (2003)

Book by Hox, Moerbeek, and Van de Schoot (2018) (textbook for the Spring 2019 class)

Book by Raudenbush and Bryk (2002) (more technical reference)

Book by Gelman and Hill (2007)

Paper by Enders and Tofighi (2007) on centering

42 / 50

Bibliography

Aitkin, M. and N. Longford (1986). "Statistical modelling issues in school effectiveness studies". In: Journal of the Royal Statistical Society. Series A (General) 149, pp. 1-43. DOI: 10.2307/2981882.

Cohen, J, P. Cohen, S. G. West, et al. (2003). Applied multiple regression/ correlation analysis for the behavioral sciences. 3rd ed. Mahwah, NJ.

Enders, C. K. and D. Tofighi (2007). "Centering predictor variables in cross-sectional multilevel models: A new look at an old issue.". In: Psychological Methods 12, pp. 121-138. DOI: 10.1037/1082-989X.12.2.121.

Gelman, A. and J. Hill (2007). Data analysis using regression and multilevel/hierarchical models. Cambridge, UK: Cambridge University Press.

Hox, J. J, M. Moerbeek and R. Van de Schoot (2018). Multilevel analysis: Techniques and applications. 3rd ed. New York, NY: Routledge.

43 / 50

Lai, M. H. C. and O. Kwok (2015). "Examining the rule of thumb of not using multilevel modeling: The “design effect smaller than two” rule". En. In: The Journal of Experimental Education 83.3, pp. 423-438. DOI: 10.1080/00220973.2014.907229.

Leeuw, J. de and I. Kreft (1986). "Random coefficient models for multilevel analysis". In: Journal of Educational Statistics 11, pp. 57-85. DOI: 10.2307/1164848.

Littell, R. C, G. A. Milliken, W. W. Stroup, et al. (1996). SAS System for mixed models. Cary, NC: SAS.

Raudenbush, S. W. and A. S. Bryk (2002). Hierarchical linear models: Applications and data analysis methods. 2nd ed. Thousand Oaks, CA: Sage.

44 / 50

Thanks!

Slides created via the R package xaringan.

45 / 50

(Unconditional) Random Intercept Model

popular score of student i in class j
= Mean popular score of class j + deviation of student i from class mean

Lv-1: popularij=β0j+eij

46 / 50

(Unconditional) Random Intercept Model

Mean popular score of class j
= Grand mean + deviation of class j from Grand mean

Lv-2: β0j=γ00+u0j

47 / 50

(Unconditional) Random Intercept Model

Overall model: popularij=γ00+u0j+eij

Fixed effects (γ00): constant for everyone

Random effects (u0j,eij): varies across clusters

  • Usually assumed normally distributed
  • Variance components: variance of random effects
48 / 50
m0 <- lmer(popular ~ (1 | class), data = popdata)
summary(m0)
## Linear mixed model fit by REML ['lmerMod']
## Formula: popular ~ (1 | class)
##    Data: popdata
## 
## REML criterion at convergence: 6330
## 
## Scaled residuals: 
##    Min     1Q Median     3Q    Max 
## -3.566 -0.698  0.002  0.676  3.318 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  class    (Intercept) 0.702    0.838   
##  Residual             1.222    1.105   
## Number of obs: 2000, groups:  class, 100
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)   5.0779     0.0874    58.1
49 / 50

Interpreting the Output

  • Estimated grand mean (ˆγ00) = 5.078
  • Estimated classroom-level variance (ˆσ2u0) = 0.702
  • Estimated student-level variance (ˆσ2e) = 1.222
  • ICC = .365
50 / 50

Different Names

Hierarchical linear model (HLM; Raudenbush and Bryk, 2002)

Mixed/Mixed-effects model (Littell, Milliken, Stroup, et al., 1996)

Random coefficient model (de Leeuw and Kreft, 1986)

Variance component model (Aitkin and Longford, 1986)

2 / 50

Ask them to introduce themselves and what research they are interested in

Like a lot of terminologies in statistics

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow