Obtaining reliability for daily diary data using multilevel factor analysis
Hok Chio (Mark) Lai, Feng Ji, Shi Chen
University of Southern California, University of California, Berkeley, Northern Arizona University
2021 IMPS
Daily Diary Data (Positive Affect)
Multiple Items
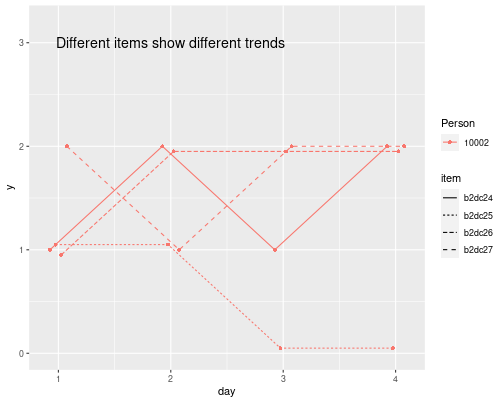
Composite/Scale Scores
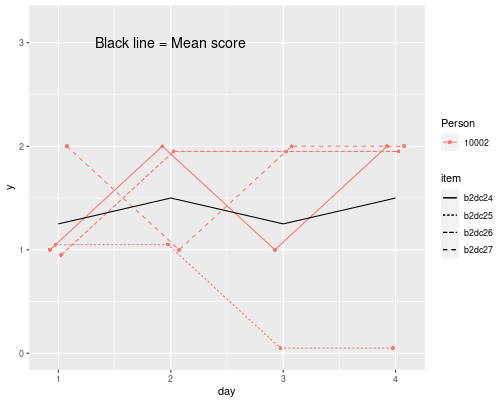
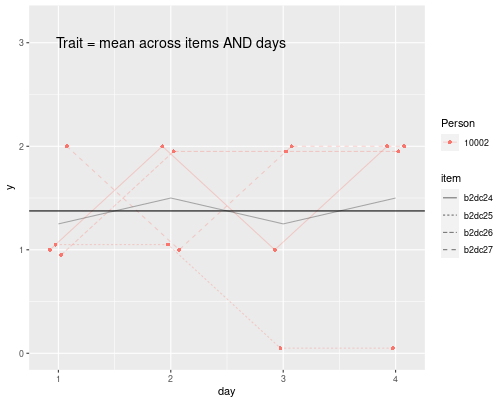
Person Mean And Deviation
Reliability is Not Commonly Reported for Diary Data
PsycInfo ("daily diary" and "emotion", peer-reviewed, 2020 July 1 to December 31)
- 15 articles; 14 with diary measures; 11 with multi-item measures
- Within-person/change reliability: 4
- Single reliability coefficient: 3
- None reported: 4
Reliability is Not Commonly Reported for Diary Data
PsycInfo ("daily diary" and "emotion", peer-reviewed, 2020 July 1 to December 31)
- 15 articles; 14 with diary measures; 11 with multi-item measures
- Within-person/change reliability: 4
- Single reliability coefficient: 3
- None reported: 4
Approaches for level-specific reliability
Generalizability theory (GT; Cranford, et al., 2006; Shrout, et al., 2012)
Multilevel factor analysis (MFA; Geldhof, et al., 2014; Lai, 2021)
Overview
GT as a special case of MFA
Reliability of person means (with sampling error)
Reliability of within-person deviations/Reliability of change
Do we have enough items?
MFA
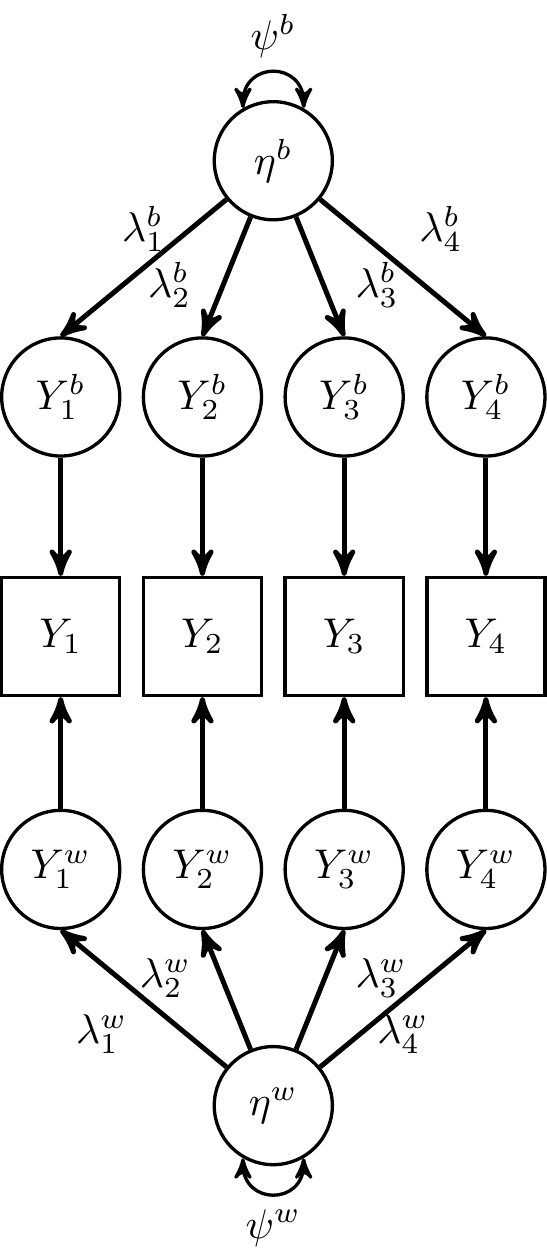
MFA

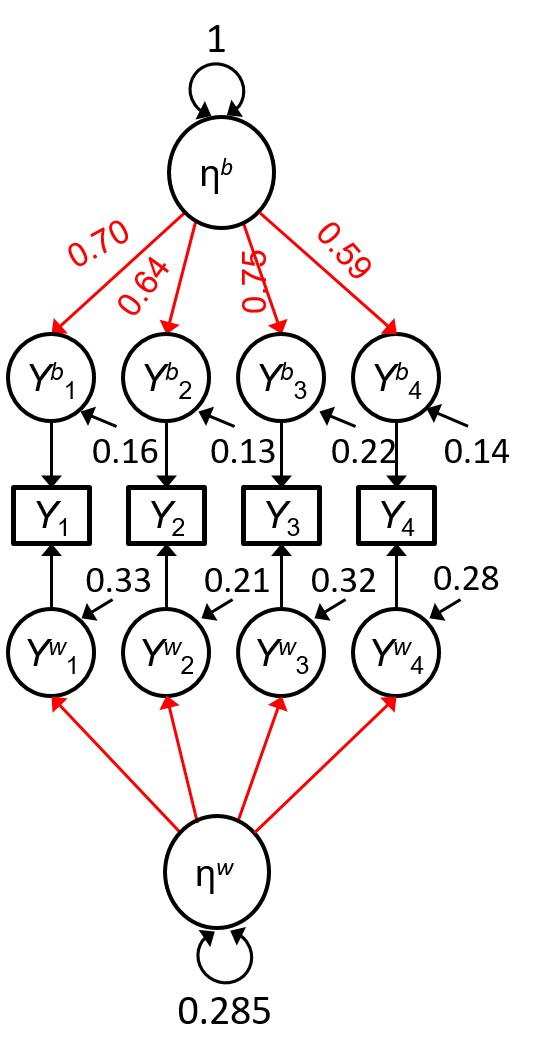
"Unconstrained" Multilevel Factor Model
i indexes person; t indexes time
Yti=ν+λbηbi+ϵbibetween model+λwiηwti+ϵwtiwithin model
GT as MFA
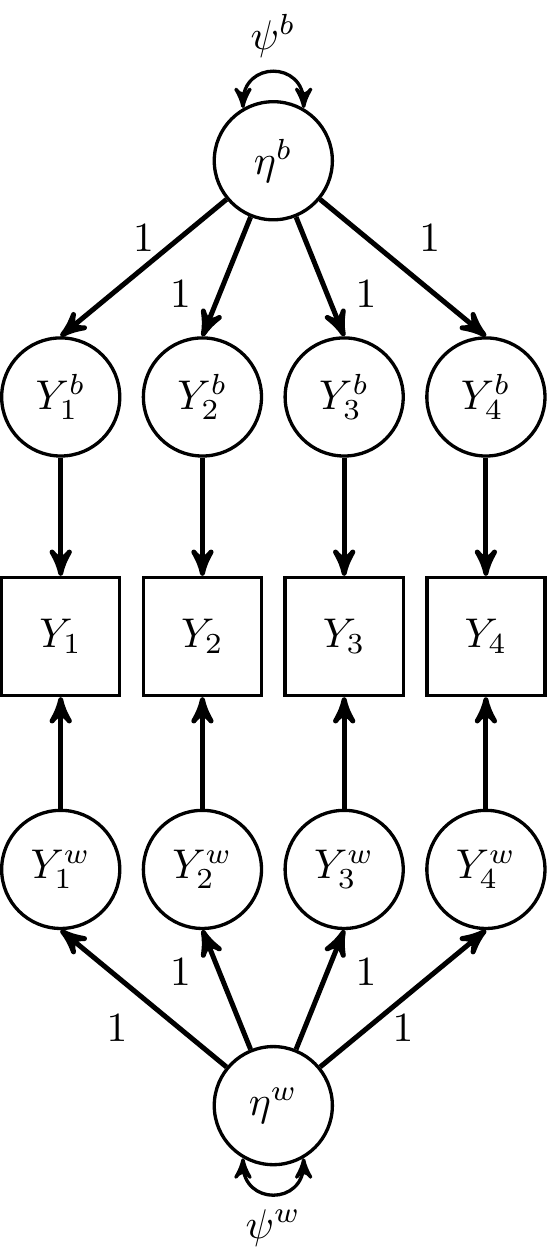
observations : (item × person)
- Here I assume no day-specific variance
(Essential) Parallel
- λbj=λwj=1
- Constant uniqueness: V(ϵbij)=θb and V(ϵwtij)=θw
GT as MFA
GT: Ytij=(μ+Ij)+Pi+(PI)ij+(TP)ti+etij
MFA: Ytij=νj+λbjηbi+ϵbij+λwijηwti+ϵwtij
Types of Observed Scores
Raw Composite: Zti=∑pj=1Ytij
Person Means: ¯Z.i=∑nt=1Zti
Person deviation: Zti−¯Z.i
n = number of time points
Reliability of Person Means (Traits)
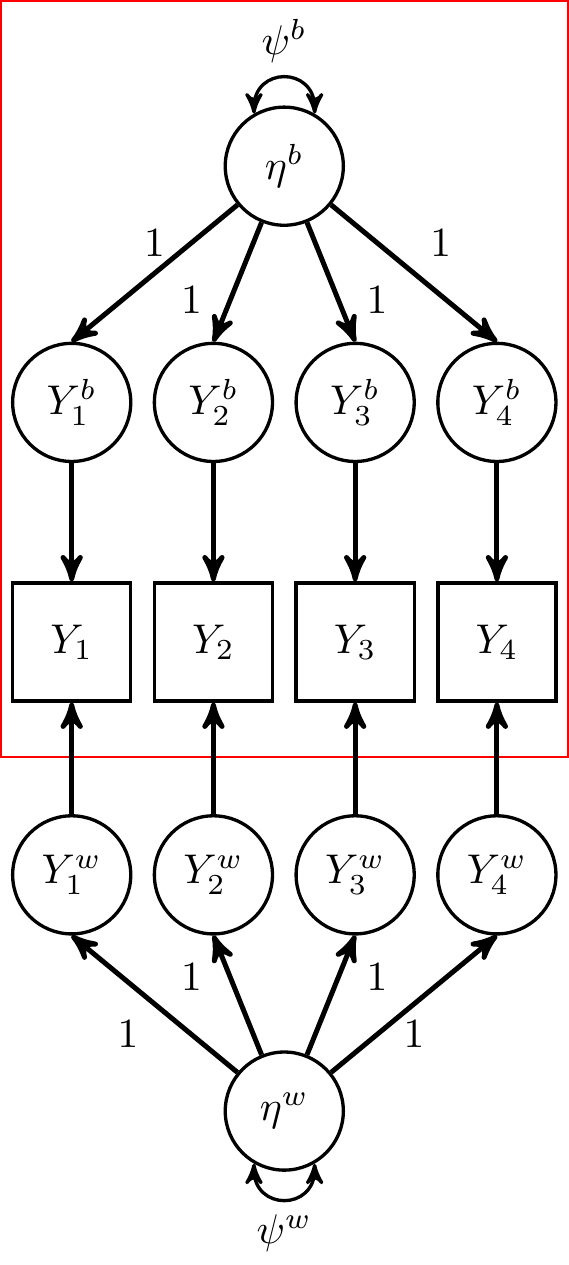
Reliability of Person Means (Traits)

Σw={σwjj′} Within covariance
Σb={σbjj′} Between covariance
Lai (2021):
αb=pp−1⎛⎜ ⎜ ⎜ ⎜ ⎜⎝∑j≠j′σbjj′1′Σb1+1′Σw1/~nsampling error⎞⎟ ⎟ ⎟ ⎟ ⎟⎠
Sample person mean of n time points is not the same as the true person mean
- Between reliability by Geldhof et al. (2014) ignores this sampling error
Reliability of Within-Person Deviations (States)
Same as reliability of change/fluctuations
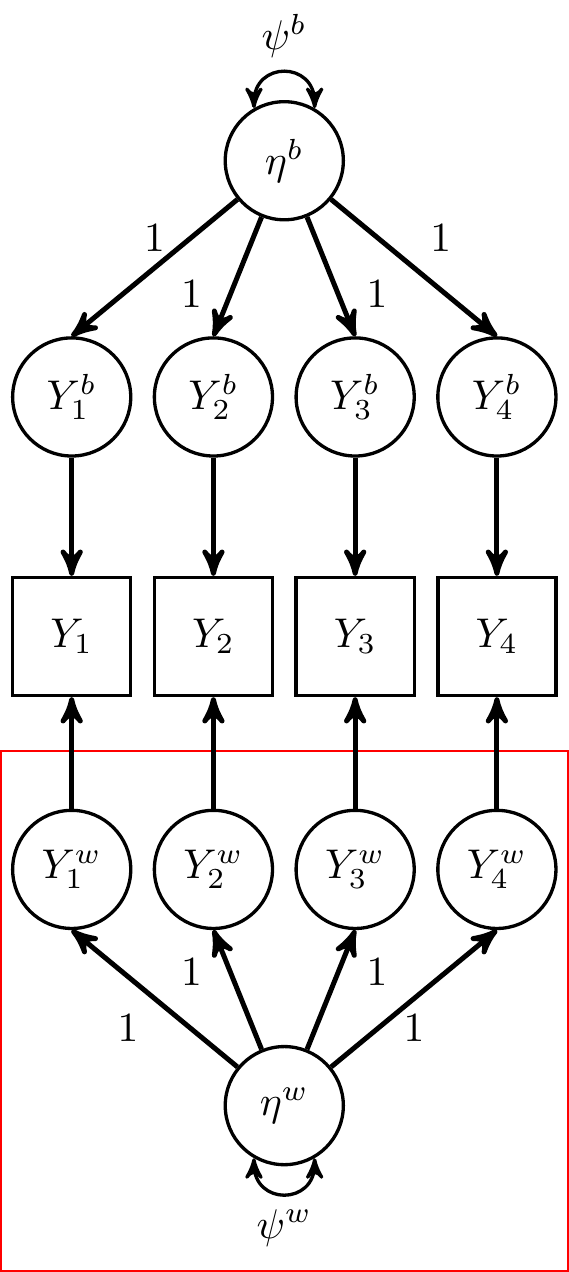
Reliability of Within-Person Deviations (States)
Same as reliability of change/fluctuations

Lai (2021):
αw=pp−1(∑k≠k′σwkk′1′Σw1)
Between and within ω reliability can be obtained by allowing different loadings across items
Example: Midlife in the United States
Data from MIDUS 2: Daily Stress Project, 2004-2009 (Ryff et al., 2009)
- 2,022 participants, 8 days each
Example: Midlife in the United States
Data from MIDUS 2: Daily Stress Project, 2004-2009 (Ryff et al., 2009)
2,022 participants, 8 days each
Target construct: Positive affect
| Item | Wording |
|---|---|
| b2dc24 | Did you feel attentive? |
| b2dc25 | Did you feel proud? |
| b2dc26 | Did you feel active? |
| b2dc27 | Did you feel confident? |
Est ICC(η)=.778
| Composite | Est α | 95% CI | Est ω | 95% CI |
|---|---|---|---|---|
| Raw | .832 | [.820, .843] | .829 | [.817, .841] |
| Within | .646 | [.628, .664] | .645 | [.625, .662] |
| Between | .862 | [.849, .873] | .860 | [.817, .872] |
Equivalence of GT and Constrained MFA
GT:
- Reliability of change (Cranford et al., 2006): V(PI)/[V(PI)+V(e)/p]
#> Rc #> 0.646Constrained MFA:
- ρw (Geldhof et al., 2014; Lai, 2021): p2ψw/(p2ψw+pθw)
#> rho^w #> 0.646p = number of items
R Function multilevel_alpha()
https://github.com/marklhc/mcfa_reliability_supp/blob/master/multilevel_alpha.R
multilevel_alpha(d2_var[c("b2dc24", "b2dc25", "b2dc26", "b2dc27")], id = d2_var$m2id)#> Parallel analysis suggests that the number of factors = NA and the number of components = 1 #> Parallel analysis suggests that the number of factors = NA and the number of components = 1#> $alpha#> alpha2l alphab alphaw #> 0.8318040 0.8616034 0.6460802 #> #> $alpha_ci#> 2.5% 97.5%#> alpha2l 0.8202014 0.8425253#> alphab 0.8488781 0.8734602#> alphaw 0.6269076 0.6638443#> #> $omega#> omega2l omegab omegaw #> 0.8293460 0.8595804 0.6445232 #> #> $omega_ci#> 2.5% 97.5%#> omega2l 0.8173008 0.8408357#> omegab 0.8461517 0.8719812#> omegaw 0.6259997 0.6620339#> #> $ncomp#> within between #> 1 1Do We Have Enough Items to Capture Change?
With 4 items, within-person reliability is only .646
Spearman-Brown formula:
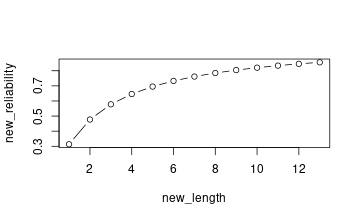
Need 6 items for αw>.70, 9 items for αw>.80
Conclusion
Reliability information needs to be more consistently reported for diary studies
- And tools are needed to make the computation more accessible
Using one or two items may not allow reliable examination of change
Esp when ICC is high
Choosing items with higher loadings may help
More scale validation in daily diary context helps researchers plan for sufficient reliability
References
Cranford, J. A. et al. (2006). "A procedure for evaluating sensitivity to within-person change: Can mood measures in diary studies detect change reliably?" In: Personality and Social Psychology Bulletin 32.7, pp. 917-929. DOI: 10.1177/0146167206287721.
Geldhof, G. J. et al. (2014). "Reliability estimation in a multilevel confirmatory factor analysis framework". In: Psychological Methods 19.1, pp. 72-91. DOI: 10.1037/a0032138.
Lai, M. H. C. (2021). "Composite reliability of multilevel data: It’s about observed scores and construct meanings." In: Psychological Methods 26 (1). DOI: 10.1037/met0000287.
Shrout, P. E. et al. (2012). "Psychometrics". In: Handbook of Research Methods for Studying Daily Life. New York, NY, US: The Guilford Press, pp. 302-320. ISBN: 978-1-60918-747-7 978-1-60918-749-1.
Thanks!
Slides created via the R package xaringan.
The chakra comes from remark.js, knitr, and R Markdown.