Reliability of Composite Scores With Multilevel Data
Hok Chio (Mark) Lai
University of Southern California
2021/05/05
Outline
Single-Level Reliability
Outline
Single-Level Reliability
Multilevel Data
- Types of composites
- Reliability indices
Outline
Single-Level Reliability
Multilevel Data
- Types of composites
- Reliability indices
Longitudinal Data?
\newcommand{\bv}[1]{\boldsymbol{\mathbf{#1}}} \DeclareMathOperator{\tr}{tr} \DeclareMathOperator{\var}{V}
Reliability
- Psychological scales are not perfect
As we know, psychological scales are not perfect. A scale measuring people's happiness usually have random errors, and sometimes systematic errors.
Reliability
Psychological scales are not perfect
Certain level of reliability needed
- Statistical analyses are not trustworthy when the numbers are not consistent
Image credit: Reliability by Nick Youngson CC BY-SA 3.0 Alpha Stock Images
As we know, psychological scales are not perfect. A scale measuring people's happiness usually have random errors, and sometimes systematic errors.
APA Journal Article Reporting Standards (JARS)
- In the Psychometrics section (Appelbaum, et al., 2018), researchers were asked to
Estimate and report values of reliability coefficients for the scores analyzed (i.e., the research's sample) (p. 7)
Similar recommendations can be found in numerous journal and methodological guidelines
Reliability
Before talking about multilevel reliability, I wanted to give just a quick introduction on the foundational work on reliability that this research relies on.
Classical Test Theory
Lord & Novick (1968)
Observed score = True score + Error
Y = T + E
T and E independent, so
\sigma^2_Y = \sigma^2_T + \sigma^2_E

The presentation today will be drawing on the classical test theory framework, as described by the classic work by Lord & Novick, which is the framework we use to define things like alpha and omega reliability.
The idea in classical test theory is that, as shown on the graph here, the measured score of a person Y, say happiness, is determined by the person's true score or true happiness level, T, and some random error E.
Notice that T and E are represented in circles as they are latent variables, meaning that they are not observables, and instead can only be inferred from the data.
Classical Test Theory
Lord & Novick (1968)
Observed score = True score + Error
Y = T + E
T and E independent, so
\sigma^2_Y = \sigma^2_T + \sigma^2_E

Reliability \rho = \dfrac{\sigma^2_T}{\sigma^2_Y} = \dfrac{\sigma^2_T}{\sigma^2_T + \sigma^2_E} = [Corr(Y, T)]^2
The presentation today will be drawing on the classical test theory framework, as described by the classic work by Lord & Novick, which is the framework we use to define things like alpha and omega reliability.
The idea in classical test theory is that, as shown on the graph here, the measured score of a person Y, say happiness, is determined by the person's true score or true happiness level, T, and some random error E.
Notice that T and E are represented in circles as they are latent variables, meaning that they are not observables, and instead can only be inferred from the data.
Composite Reliability
(Essential) Tau Equivalence
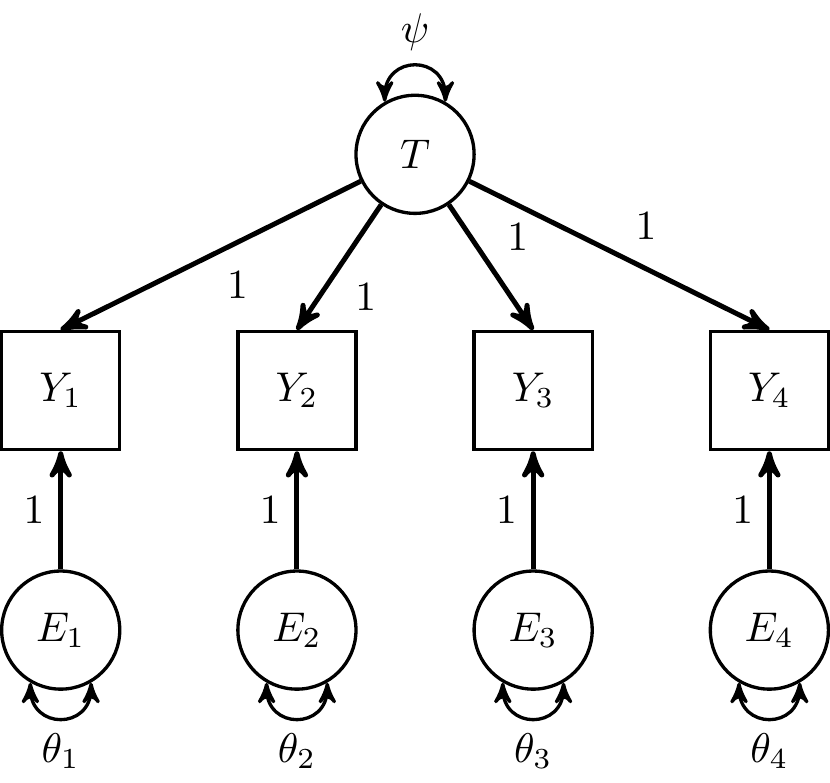
That is the case when we only have one item to measure happiness. When we have multiple items, say four items here, usually what we do is to assume that each item is an indicator of the true happiness construct. This is the idea of a factor model as represented in this figure.
The tau equivalence assumption here means that the items all have loadings of 1, meaning that the true score variance in each item is the same.
Composite Reliability
(Essential) Tau Equivalence


That is the case when we only have one item to measure happiness. When we have multiple items, say four items here, usually what we do is to assume that each item is an indicator of the true happiness construct. This is the idea of a factor model as represented in this figure.
The tau equivalence assumption here means that the items all have loadings of 1, meaning that the true score variance in each item is the same.
\alpha Reliability
Variance of unweighted composite: \var(Z) = p^2 \psi + \sum_k \theta_k
\alpha Reliability
Variance of unweighted composite: \var(Z) = p^2 \psi + \sum_k \theta_k Reliability \alpha = \dfrac{p^2 \psi}{\var(p^2 \psi + \sum_k \theta_k)}
There were different ways to justify the derivation of \alpha
\alpha Reliability
Variance of unweighted composite: \var(Z) = p^2 \psi + \sum_k \theta_k Reliability \alpha = \dfrac{p^2 \psi}{\var(p^2 \psi + \sum_k \theta_k)}
Alternative form: \alpha = \dfrac{p}{p - 1} \left(1 - \dfrac{\tr(\bv \Sigma)}{\bv 1' \bv \Sigma \bv 1}\right)
There were different ways to justify the derivation of \alpha
The idea is that we can simply use the covariance matrix of the items to compute reliability, without the need to do a factor analysis.
Composite Reliability
Congeneric
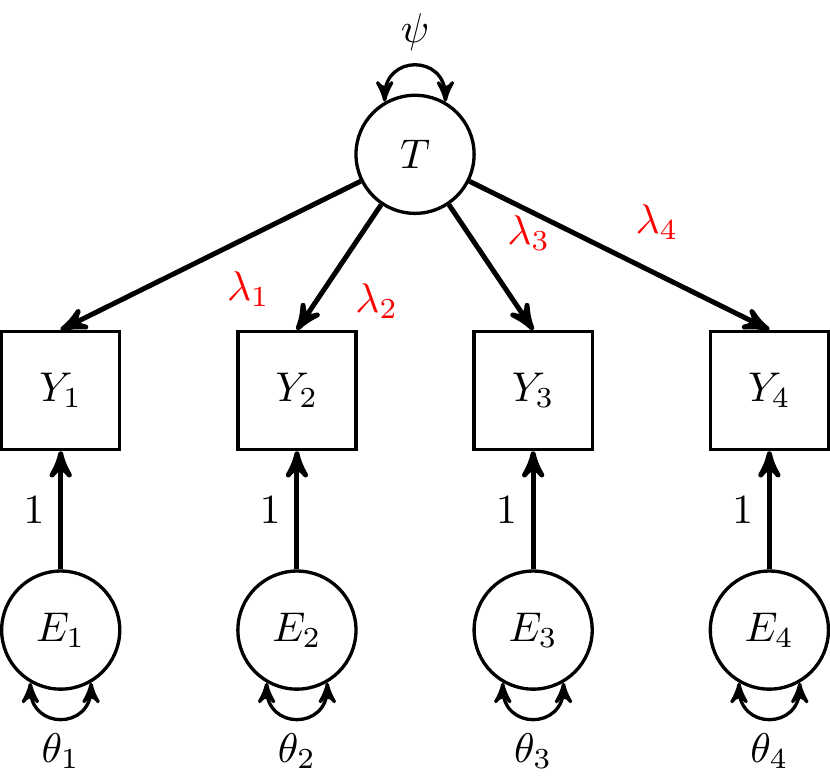
Composite Reliability
Congeneric

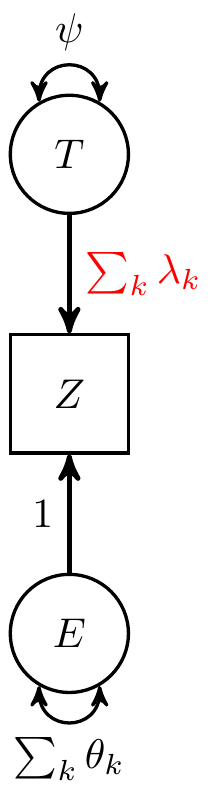
\omega Reliability
True Score Variance \var(T) = (\sum_k \lambda_k)^2 \psi
Error Variance \var(E) = \sum_k \theta_k
Reliability \omega = \dfrac{\var(T)}{\var(T) + \var(E)}
\omega Reliability
True Score Variance \var(T) = (\sum_k \lambda_k)^2 \psi
Error Variance \var(E) = \sum_k \theta_k
Reliability \omega = \dfrac{\var(T)}{\var(T) + \var(E)}
Note: Reliability is a property of observed test scores (Z), not the latent scores (\eta)
Multilevel Reliability
Lai (2021)
Example
2007 Trends in International Mathematics and Science Study (TIMSS; Williams et al., 2009)
- 7,896 students (4th grade) from 515 schools
Positive attitudes toward math (PATM)
| Item | Wording |
|---|---|
| AS4MAMOR | Would like to do more math |
| AS4MAENJ | I enjoy learning mathematics |
| AS4MALIK | I like math |
| AS4MABOR | Math is boring (reverse-coded) |
With this kind of multilevel data, in analysis we need to account for the clustering structure, as it violates the independent observation assumptions; otherwise the statistical inferences will be incorrect.
Multilevel Reliability Not Consistently Reported
Kim et al. (2016): Only 54% reported reliability, among 39 articles using multilevel confirmatory factor analysis (MCFA)
- Usually only one reliability reported for one scale
However, discussion on multilevel reliability is not new
Reliability Options in the Literature
Ignore clustering
Omit uncertainty (SE too small/CI too narrow)
- Can use multilevel factor analysis (Raykov, et al., 2005; Raykov, et al., 2006)
No level-specific information
Level-Specific Reliability (Geldhof, et al., 2014)
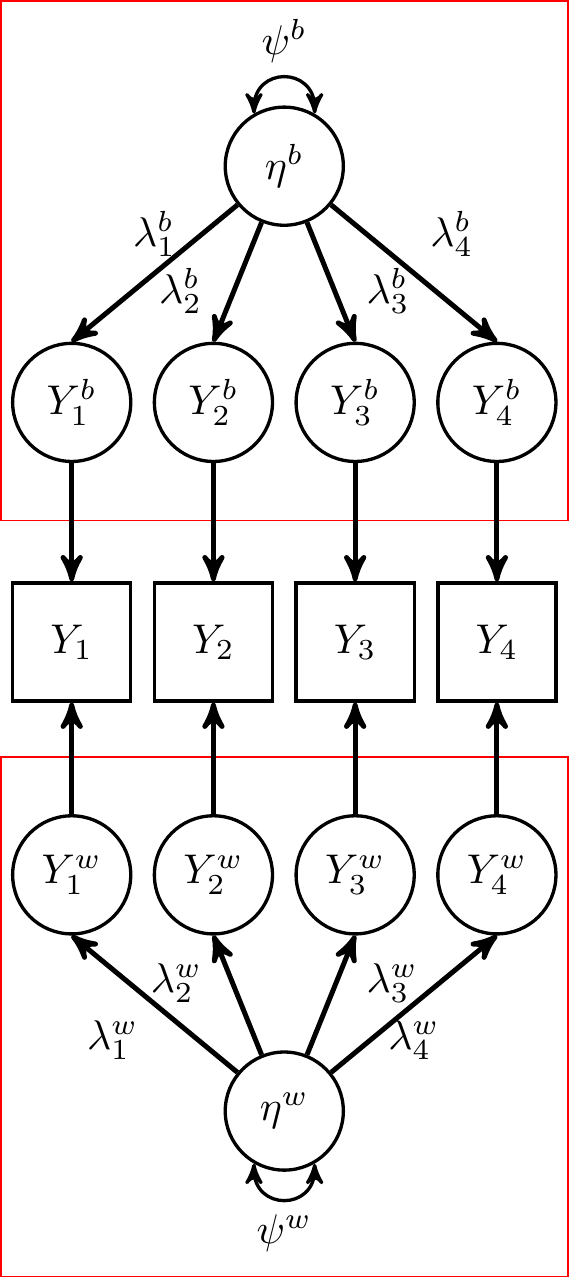
Level-Specific Reliability (Geldhof, et al., 2014)

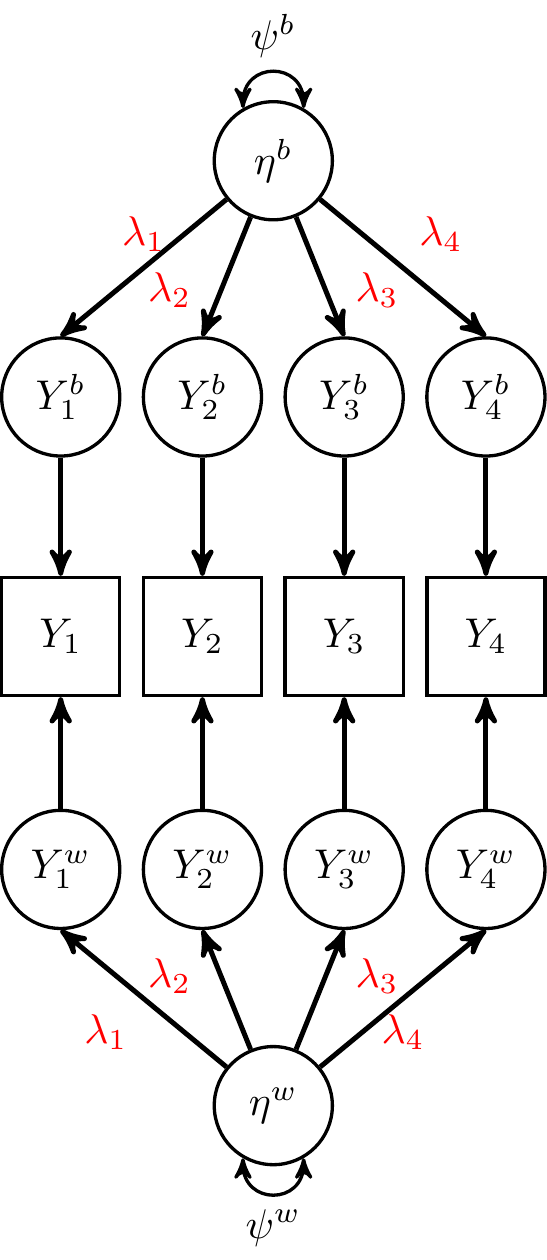
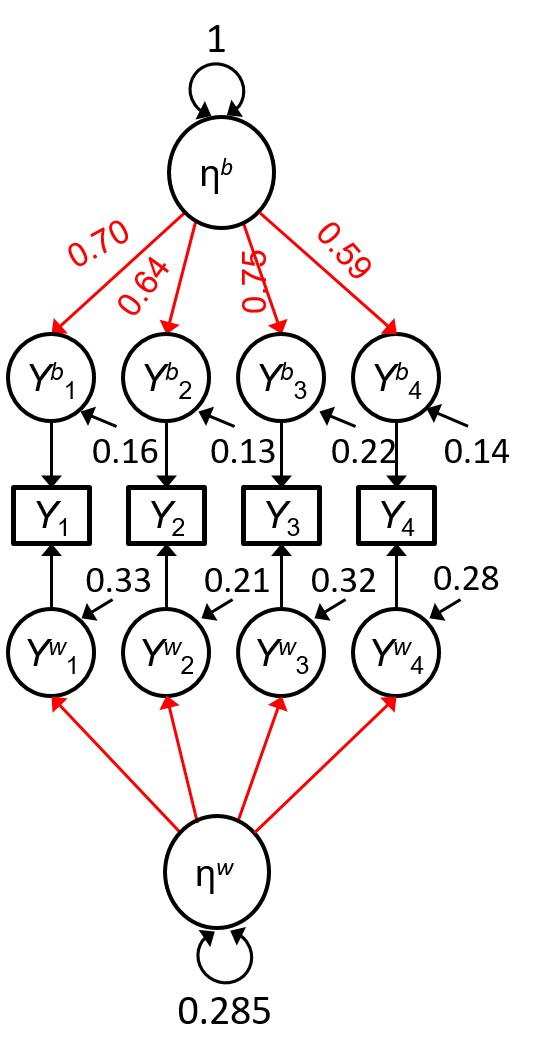
"Unconstrained" Multilevel Factor Model
j indexes cluster
\bv Y_{ij} = \bv \nu + \underbrace{\bv \lambda^b \eta^b_j + \bv \epsilon^b_{j}}_\text{between model} + \underbrace{\bv \lambda^w_j \eta^w_{ij} + \bv \epsilon^w_{ij}}_\text{within model}
- Between- and within- "reliability" coefficients
No cross-level invariance
\epsilon is the uniqueness, separated into the within and the between level
For the TIMSS data
Est \tilde \omega^w = .857, 95% CI [.849, .863]
Est \tilde \omega^b = .977, 95% CI [.964, .987]
For the TIMSS data
Est \tilde \omega^w = .857, 95% CI [.849, .863]
Est \tilde \omega^b = .977, 95% CI [.964, .987]
Not uncommon in the literature . . .
For the TIMSS data
Est \tilde \omega^w = .857, 95% CI [.849, .863]
Est \tilde \omega^b = .977, 95% CI [.964, .987]
Not uncommon in the literature . . .
Positive and negative affects: \tilde \omega^b = .94 to .97 (Rush, et al., 2014)
Instructional Skills Questionnaire: \tilde \alpha^b between .90 to .99 (Knol, et al., 2016)
Repeated measures within persons
Multiple factors in ISQ, Team from Netherlands
What Went Wrong?
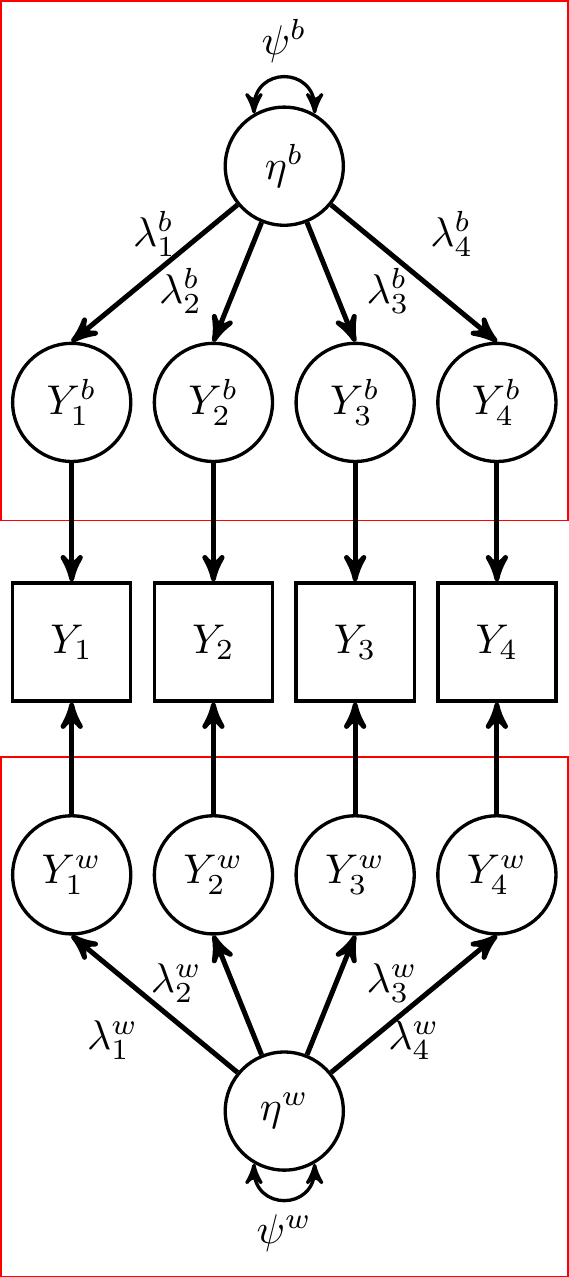
What Went Wrong?

Y_1^b and Y_1^w are not observed scores!
Observed school mean \neq True school mean (unless n_j is large; Raudenbush, et al., 2002)
Lai, M. H. C. (2021). "Composite reliability of multilevel data: It’s about observed scores and construct meanings." In: Psychological Methods 26 (1). DOI: 10.1037/met0000287.
What Are the Observed Scores With Multilevel Analysis?
What Are the Observed Scores With Multilevel Analysis?
- Raw/Overall composite (Z_{ij})
- Composite school means of (cluster mean; Z^b_j)
- Composite student deviations (cluster-mean centered; Z^w_{ij} = Z_{ij} - Z^b_j)
| IDSCHOOL | AS4MAMOR | AS4MAENJ | AS4MALIK | AS4MABORr | Z | Zb | Zw |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 2 | 1 | 2 | 7 | 6.5000 | 0.5000 |
| 1 | 2 | 1 | 1 | 1 | 5 | 6.5000 | -1.5000 |
| 1 | 2 | 1 | 1 | 1 | 5 | 6.5000 | -1.5000 |
| 1 | 2 | 1 | 2 | 1 | 6 | 6.5000 | -0.5000 |
| 1 | 1 | 1 | 1 | 1 | 4 | 6.5000 | -2.5000 |
| 2 | 3 | 2 | 2 | 2 | 9 | 6.5625 | 2.4375 |
| 2 | 1 | 2 | 2 | 1 | 6 | 6.5625 | -0.5625 |
| 2 | 1 | 1 | 1 | 1 | 4 | 6.5625 | -2.5625 |
| 2 | 3 | 2 | 1 | 1 | 7 | 6.5625 | 0.4375 |
| 2 | 2 | 2 | 3 | 1 | 8 | 6.5625 | 1.4375 |
Sampling Error of School Means

Multilevel \alpha and \omega Reliability Indices
Variance Components in Reliability Coefficients
Variance Components in Reliability Coefficients
Within \frac{\var(T^w)}{\var(T^w) + \var(E^w)}
Variance Components in Reliability Coefficients
Within \frac{\var(T^w)}{\var(T^w) + \var(E^w)}
Between \frac{\var(T^b)}{\var(T^b) + \var(E^b) + \underbrace{\color{red}{[\var(T^w) + \var(E^w)] / n}}_{\text{sampling error}}}
Variance Components in Reliability Coefficients
Within \frac{\var(T^w)}{\var(T^w) + \var(E^w)}
Between \frac{\var(T^b)}{\var(T^b) + \var(E^b) + \underbrace{\color{red}{[\var(T^w) + \var(E^w)] / n}}_{\text{sampling error}}}
Raw \frac{\var(T^w) + \var(T^b)}{\var(T^w) + \var(E^w) + \var(T^b) + \var(E^b)}
Extensions of \alpha
First, obtain estimated covariance matrices at the between (\Sigma^b) and the within levels (\Sigma^w)
Extensions of \alpha
First, obtain estimated covariance matrices at the between (\Sigma^b) and the within levels (\Sigma^w)
\begin{align*} \alpha^{2l} & = \frac{p}{p - 1}\left(\frac{\sum_{k \neq k'} (\sigma^{b}_{k k'} + \sigma^{w}_{k k'})}{\bv 1'\bv \Sigma^b \bv 1 + \bv 1' \bv \Sigma^w \bv 1}\right) \\ \alpha^{b} & = \frac{p}{p - 1}\left(\frac{\sum_{k \neq k'} \sigma^{b}_{k k'}}{\bv 1'\bv \Sigma^b \bv 1 + \bv 1' \bv \Sigma^w \bv 1 / \tilde n}\right) \\ \alpha^{w} & = \frac{p}{p - 1}\left(\frac{\sum_{k \neq k'} \sigma^{w}_{k k'}}{\bv 1' \bv \Sigma^w \bv 1}\right) \end{align*}
\tilde n = harmonic mean of cluster sizes (e.g., number of students in each school in the sample)
Extensions of \omega
Depends on the model
- Cross-level invariance (Jak, et al., 2014; Mehta, et al., 2005)
Other Model Considerations
Unidimensionality
- Can be assessed using parallel analysis on the between- and within- correlation matrices (Y. Ji et al., in preparation)
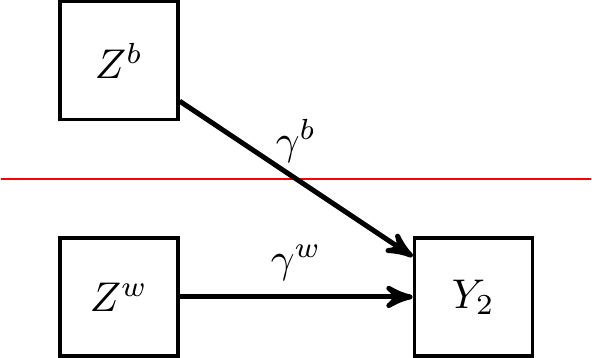
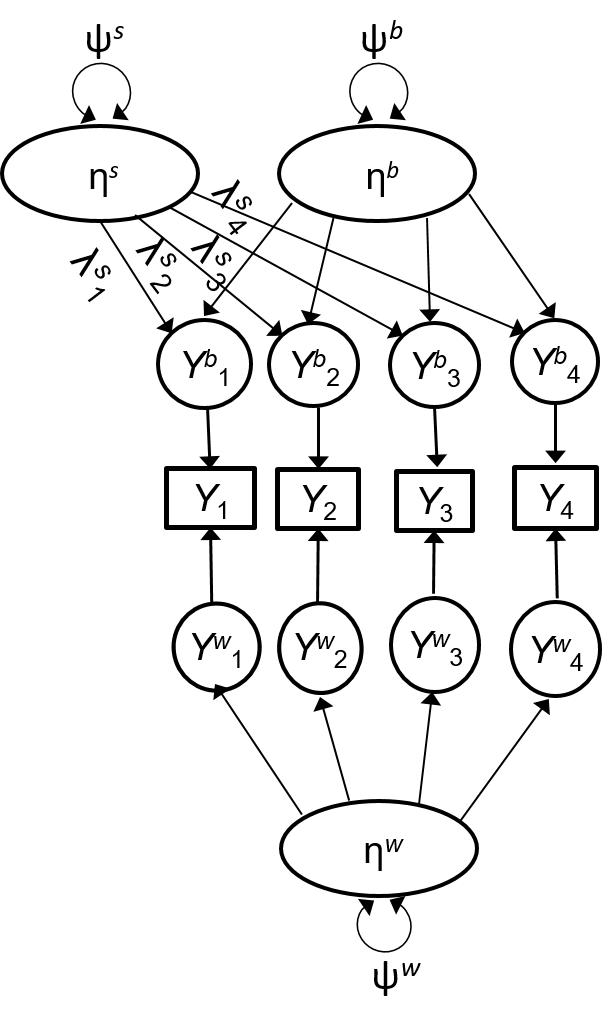
"Shared" construct (Stapleton, et al., 2016; Stapleton, et al., 2019)
- E.g., Use aggregated student ratings to measure teacher qualities
- Between-level composite may measure both teacher effectiveness + acquiescence

Which One(s) to Report?
If a variable is partitioned in a multilevel model (most likely an individual construct), all three (\omega^{2l}, \omega^{b}, \omega^{w}) should be reported
Cluster means and cluster-mean centered predictors
Outcome variable
Which One(s) to Report?
If a variable is partitioned in a multilevel model (most likely an individual construct), all three (\omega^{2l}, \omega^{b}, \omega^{w}) should be reported
Cluster means and cluster-mean centered predictors
Outcome variable
R Function multilevel_reliability()
multilevel_reliability( timss_usa[c("AS4MAMOR", "AS4MAENJ", "AS4MALIK", "AS4MABORr")], id = timss_usa$IDSCHOOL)## Parallel analysis suggests that the number of factors = NA and the number of components = 1 ## Parallel analysis suggests that the number of factors = NA and the number of components = 1## $alpha## alpha2l alphab alphaw ## 0.8675110 0.6527865 0.8592387 ## ## $alpha_ci## 2.5% 97.5%## alpha2l 0.8604497 0.8741798## alphab 0.5802825 0.7046562## alphaw 0.8517564 0.8663573## ## $omega## omega2l omegab omegaw ## 0.8674844 0.6233126 0.8605125 ## ## $omega_ci## 2.5% 97.5%## omega2l 0.8602266 0.8739374## omegab 0.5501061 0.6761630## omegaw 0.8529576 0.8672256## ## $ncomp## within between ## 1 1Longitudinal Data
Lai, F. Ji, & Chen (in preparation). Suggestions greatly appreciated.
Midlife in the United States
Data from MIDUS 2: Daily Stress Project, 2004-2009 (Ryff, et al., 2009)
- 2,022 participants, 8 days each
Midlife in the United States
Data from MIDUS 2: Daily Stress Project, 2004-2009 (Ryff, et al., 2009)
2,022 participants, 8 days each
Target construct: Positive affect
| Item | Wording |
|---|---|
| b2dc24 | Did you feel attentive? |
| b2dc25 | Did you feel proud? |
| b2dc26 | Did you feel active? |
| b2dc27 | Did you feel confident? |
Midlife in the United States
Data from MIDUS 2: Daily Stress Project, 2004-2009 (Ryff, et al., 2009)
2,022 participants, 8 days each
Target construct: Positive affect
| Item | Wording |
|---|---|
| b2dc24 | Did you feel attentive? |
| b2dc25 | Did you feel proud? |
| b2dc26 | Did you feel active? |
| b2dc27 | Did you feel confident? |
- Type of scores: raw composite, person means, person-mean centered
From MCFA
Est \text{ICC}(\eta) = .778
| Composite | Est \alpha | 95% CI | Est \omega | 95% CI |
|---|---|---|---|---|
| Raw | .832 | [.820, .843] | .829 | [.817, .841] |
| Within | .646 | [.628, .664] | .645 | [.625, .662] |
| Between | .862 | [.849, .873] | .860 | [.817, .872] |
From MCFA
Est \text{ICC}(\eta) = .778
| Composite | Est \alpha | 95% CI | Est \omega | 95% CI |
|---|---|---|---|---|
| Raw | .832 | [.820, .843] | .829 | [.817, .841] |
| Within | .646 | [.628, .664] | .645 | [.625, .662] |
| Between | .862 | [.849, .873] | .860 | [.817, .872] |

However, the model assumes no time-specific variances and covariances
Incorporating Time
Cross-Classified CFA (Jeon, et al., 2012; Asparouhov, et al., 2016)
Assuming cross-level invariance for an individual construct, with decomposition \eta_{ti} = \eta^{(P)}_i + \eta^{(T)}_t + \eta^{(W)}_{ti}
W = P x T + Error
Bayesian Estimation in Stan
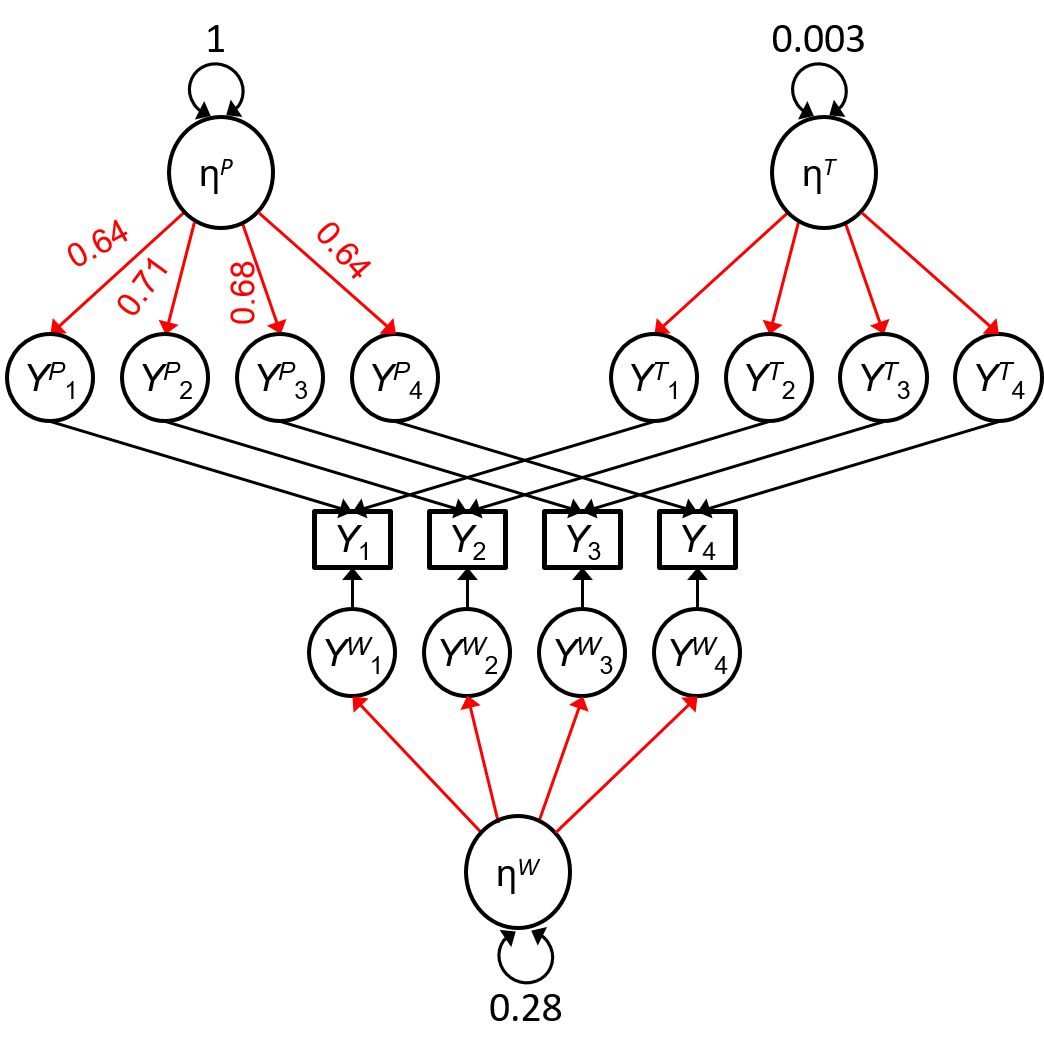
With the MIDUS daily diary data, there is essentially no time-level variance
- E.g., no day of participation effect
With the MIDUS daily diary data, there is essentially no time-level variance
- E.g., no day of participation effect
Reliability coefficients remain the same when modeling the time-level variance
Many Questions Remain
- Discrete indicators?
Many Questions Remain
Discrete indicators?
Should we treat within-person and between-person constructs as parts of one construct?
- Local homogeneity assumption (Ellis, et al., 1993)
Many Questions Remain
Discrete indicators?
Should we treat within-person and between-person constructs as parts of one construct?
- Local homogeneity assumption (Ellis, et al., 1993)
Time-varying reliability?
- Martin & Rast (2020, PsyArXiv)
Many Questions Remain
Discrete indicators?
Should we treat within-person and between-person constructs as parts of one construct?
- Local homogeneity assumption (Ellis, et al., 1993)
Time-varying reliability?
- Martin & Rast (2020, PsyArXiv)
Are there "shared" constructs at the person level?
- E.g., response bias --> item scores more correlated at the between level
Summary
Computing and reporting reliability information is important for multilevel data
- Both cross-sectional and longitudinal
Summary
Computing and reporting reliability information is important for multilevel data
- Both cross-sectional and longitudinal
Reliability information is needed for raw, cluster means, and cluster-mean centered scores
Summary
Computing and reporting reliability information is important for multilevel data
- Both cross-sectional and longitudinal
Reliability information is needed for raw, cluster means, and cluster-mean centered scores
Previous approach to between-level reliability is an overestimate when cluster size is small
Summary
Computing and reporting reliability information is important for multilevel data
- Both cross-sectional and longitudinal
Reliability information is needed for raw, cluster means, and cluster-mean centered scores
Previous approach to between-level reliability is an overestimate when cluster size is small
Nature of target construct should be considered, and it has implications on reliability computation
- E.g., "shared" constructs
Acknowledgement
Collaborators: Feng Ji (UC Berkeley) and Shi Chen (Northern Arizona University)
Oi-man Kwok and Hio Wa Mak for suggestions on the paper
References
Appelbaum, M. et al. (2018). "Journal article reporting standards for quantitative research in psychology". In: American Psychologist 73.1, pp. 3-25. DOI: 10.1037/amp0000191.
Asparouhov, T. et al. (2016). "General random effect latent variable modeling: Random subjects, items, contexts, and parameter". In: Advances in multilevel modeling for educational research: Addressing practical issues found in real-world applications. Charlotte, NC: Information Age, pp. 163-192.
Ellis, J. L. et al. (1993). "Local homogeneity in latent trait models. A characterization of the homogeneous monotone irt model". In: Psychometrika 58.3, pp. 417-429. DOI: 10.1007/bf02294649.
Geldhof, G. J. et al. (2014). "Reliability estimation in a multilevel confirmatory factor analysis framework". In: Psychological Methods 19.1, pp. 72-91. DOI: 10.1037/a0032138.
References (cont'd)
Jak, S. et al. (2014). "Measurement bias in multilevel data". In: Structural Equation Modeling: A Multidisciplinary Journal 21.1, pp. 31-39. DOI: 10.1080/10705511.2014.856694.
Jeon, M. et al. (2012). "Profile-likelihood approach for estimating generalized linear mixed models with factor structures". In: Journal of Educational and Behavioral Statistics 37.4, pp. 518-542. DOI: 10.3102/1076998611417628.
Knol, M. H. et al. (2016). "Measuring the quality of university lectures: Development and validation of the Instructional Skills Questionnaire (ISQ)". In: PLOS ONE 11.2. Ed. by D. S. Courvoisier, p. e0149163. DOI: 10.1371/journal.pone.0149163.
Lai, M. H. C. (2021). "Composite reliability of multilevel data: It’s about observed scores and construct meanings." In: Psychological Methods 26 (1). DOI: 10.1037/met0000287.
References (cont'd)
Mehta, P. D. et al. (2005). "People are variables too: Multilevel structural equations modeling". In: Psychological Methods 10.3, pp. 259-284. DOI: 10.1037/1082-989X.10.3.259.
Raudenbush, S. W. et al. (2002). Hierarchical linear models: Applications and data analysis methods. 2nd ed. Thousand Oaks, CA: Sage. ISBN: 076191904X.
Raykov, T. et al. (2006). "On multilevel model reliability estimation from the perspective of structural equation modeling". In: Structural Equation Modeling: A Multidisciplinary Journal 13.1, pp. 130-141. DOI: 10.1207/s15328007sem1301_7.
Raykov, T. et al. (2005). "Estimation of reliability for multiple-component measuring instruments in hierarchical designs". In: Structural Equation Modeling: A Multidisciplinary Journal 12.4, pp. 536-550. DOI: 10.1207/s15328007sem1204_2.
References (cont'd)
Rush, J. et al. (2014). "Differences in within- and between-person factor structure of positive and negative affect: Analysis of two intensive measurement studies using multilevel structural equation modeling.". In: Psychological Assessment 26.2, pp. 462-473. DOI: 10.1037/a0035666.
Ryff, C. D. et al. (2009). Midlife in the United States (MIDUS 2): Daily Stress Project, 2004-2009: Version 2. type: dataset. DOI: 10.3886/ICPSR26841.V2.
Stapleton, L. M. et al. (2019). "Models to Examine the Validity of Cluster-Level Factor Structure Using Individual-Level Data". In: Advances in Methods and Practices in Psychological Science 2.3, pp. 312-329. DOI: 10.1177/2515245919855039.
Stapleton, L. M. et al. (2016). "Construct meaning in multilevel settings". In: Journal of Educational and Behavioral Statistics 41.5, pp. 481-520. DOI: 10.3102/1076998616646200.
Influence of ICC and Cluster Size
Assume cross-level invariance holds and \omega^{2l} = .8
\mathrm{ICC}(\eta) = \frac{\psi^b}{\psi^b + \psi^w}

Relation to Generalizability Theory
Most meaningful with systematic time effects
Cranford, et al. (2006): generalizability coefficients for diary studies
Not the case for the MIDUS data, as everyone starts on a different day
Relation to Generalizability Theory
Most meaningful with systematic time effects
Cranford, et al. (2006): generalizability coefficients for diary studies
Differences:
- Fixed vs. Random item facet (in estimation)
Not the case for the MIDUS data, as everyone starts on a different day
Relation to Generalizability Theory
Most meaningful with systematic time effects
Cranford, et al. (2006): generalizability coefficients for diary studies
Differences:
Fixed vs. Random item facet (in estimation)
Relax the essential parallel test assumption
- Item-specific loadings and uniqueness
Not the case for the MIDUS data, as everyone starts on a different day
Relation to Generalizability Theory
Most meaningful with systematic time effects
Cranford, et al. (2006): generalizability coefficients for diary studies
Differences:
Fixed vs. Random item facet (in estimation)
Relax the essential parallel test assumption
- Item-specific loadings and uniqueness
- Test invariance assumptions
Not the case for the MIDUS data, as everyone starts on a different day
Relation to Generalizability Theory
Most meaningful with systematic time effects
Cranford, et al. (2006): generalizability coefficients for diary studies
Differences:
Fixed vs. Random item facet (in estimation)
Relax the essential parallel test assumption
- Item-specific loadings and uniqueness
Test invariance assumptions
Flexible SEM modeling
Not the case for the MIDUS data, as everyone starts on a different day