Advancing Quantitative Science

class: center, middle, inverse, title-slide

# Advancing Quantitative Science
## with Monte Carlo Simulation
<html>
<div style="float:left">

</div>
<hr color='#EB811B' size=1px width=796px>
</html>
### Hok Chio (Mark) Lai
### 2019/05/16

---

# Monte Carlo Methods

.pull-left[
- 1930s-1940s: Nuclear physics
   * Key figures:
       * Stanislaw Ulam
       * John von Neumann
       * Nicholas Metropolis
   * Manhattan project: hydrogen bomb
- Naming: Casino in Monaco
]

.pull-right[
![](images/Casino_Monte_Carlo.png)
]

---

# Why Do We Do Statistics?

- To study some target quantities in the population
    * Based on a limited sample
- How do we know that a statistics/statistical method gets us to a reasonable answer?
    * Analytic reasoning
    * Simulation

---
class: inverse, center, middle

# MC is one way to understand the properties of one or more statistical procedures

---

# What is MC (in Statistics)?

- Simulate the _process of repeated random sampling_
    * E.g., repeatedly drawing sample of IQ scores of size 10 from a population
- Approximate _sampling distributions_
    * Using __pseudorandom samples__
- Study properties of __estimators__
    * regression coefficients, fit index
    * compare multiple estimators or modeling approaches

---

# What is it (cont'd)?

- Based on Carsey & Harden (2014):
    * Simulations as experiments
        * Whether there's a "treatment" effect (but not why)
    * Simulations help develop intuition
        * Shouldn't replace analytically and theoretical reasoning 
    * Simulations help evaluate substantive theories and empirical results

???

Sometimes analytic solution does not exist

---

# Examples in the Literature

- [Curran, West, & Finch (1996, Psych Methods)](http://dx.doi.org/10.1037/1082-989X.1.1.16) studied the performance of the `\(\chi^2\)` test for nonnormal data in CFA
- [Kim & Millsap (2014, MBR)](http://dx.doi.org/10.1080/00273171.2014.947352) studied the performance of the Bollen-Stine Bootstrapping method for evaluating SEM fit indices
- [MacCallum, Widaman, Zhang, & Hong (1999, Psych Methods)](http://dx.doi.org/10.1037/1082-989X.4.1.84) studied sample size requirement for getting stable EFA results
- [Maas & Hox (2005, Methodology)](http://dx.doi.org/10.1027/1614-2241.1.3.86) studied the sample size requirement for multilevel models

---

# Generating Random Data in R

With MC, one simulates the process of generating the data with an assumed 
__data generating model__

- Model: including both functional form and distributional assumptions

.font80[

```r
rnorm(5, mean = 0, sd = 1)
```

```
## [1]  0.8863733  1.6361050 -1.3694538 -1.1621330  1.1365392
```

```r
rnorm(5, mean = 0, sd = 1)  # number changed
```

```
## [1]  0.6607360 -0.7283291  0.5751322  1.4180376 -1.5442535
```
]

---

# Setting the Seed

- Most programs use algorithms to generate numbers that look like random
    * _pseudorandom_
    * Completely determined by the _seed_
- For replicability, <font color="red">__ALWAYS__</font> explicitly set the seed
in the beginning

.font80[

```r
set.seed(1)
rnorm(5, mean = 0, sd = 1)
```

```
## [1] -0.6264538  0.1836433 -0.8356286  1.5952808  0.3295078
```

```r
set.seed(1)
rnorm(5, mean = 0, sd = 1)  # same seed, same number
```

```
## [1] -0.6264538  0.1836433 -0.8356286  1.5952808  0.3295078
```
]

---

# Generating Data From Univariate Distributions

```r
rnorm(n, mean, sd)      # Normal distribution (mean and SD)
runif(n, min, max)      # Uniform distribution (minimum and maximum)
rchisq(n, df)           # Chi-squared distribution (degrees of freedom)
rbinom(n, size, prob)   # Binomial distribution
```

???

Other distributions include `exponential`, `gamma`, `beta`, `t`, `F`

---

# MC Approximation of `\(\mathcal{N}(0, 1)\)`

.small[

```r
library(tidyverse)
set.seed(123)
nsim <- 20  # 20 samples
sam <- rnorm(nsim)  # default is mean = 0 and sd = 1
ggplot(tibble(x = sam), aes(x = x)) + 
  geom_density(bw = "SJ") + 
  stat_function(fun = dnorm, col = "red")  # overlay normal curve in red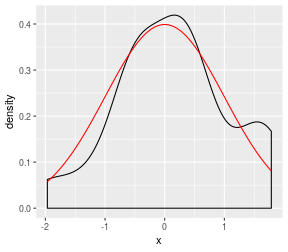
```

![](2019mc_slides_files/figure-html/unnamed-chunk-2-1.png)
]

---
class: inverse

# Exercise

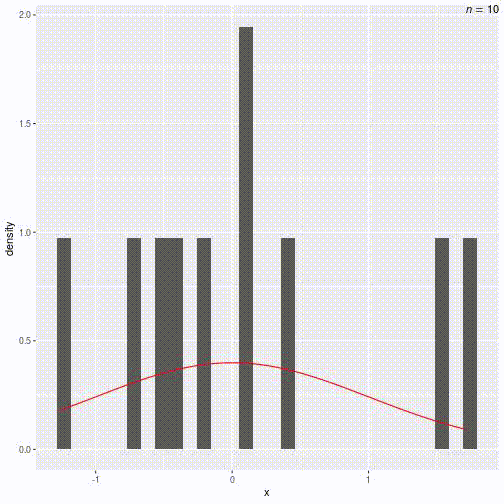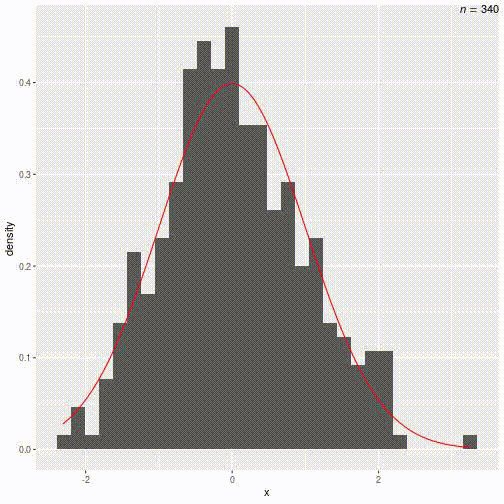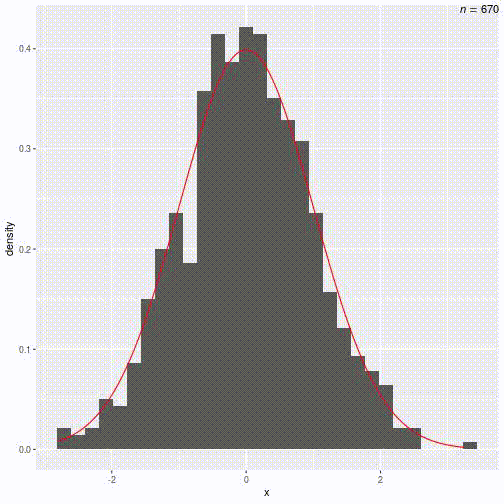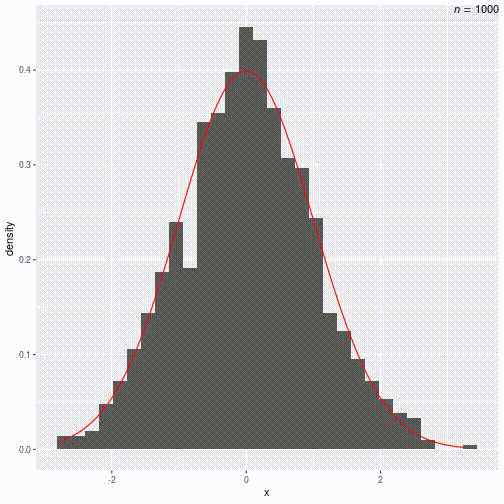
Try increasing `nsim` to 100, then 1,000

---

# Exercise

![](2019mc_slides_files/figure-html/unnamed-chunk-3.gif)

---

# Parameter vs Estimator

- __Estimator__/statistic: `\(T(\mathbf{X})\)`, or simply `\(T\)`
    * How good does it estimate the population parameter, `\(\theta\)`?
- Examples:
    * `\(T = \bar{X}\)` estimates `\(\theta = \mu\)`
    * `\(T = \dfrac{\sum_i (X_i - \bar{X})^2}{N - 1}\)` estimates `\(\theta = \sigma^2\)`

---

# Properties of Estimators

- Bias
- Consistency
- Efficiency
- Robustness

---

# What is a Good Estimator?

![](images/bias&efficiency.png)

---

# Sampling Distribution

- What is it?

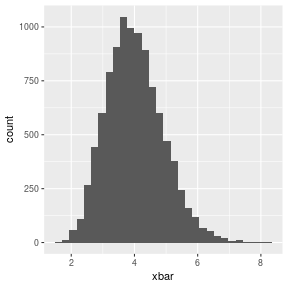
![](2019mc_slides_files/figure-html/unnamed-chunk-4-1.png)

---
class: inverse, center, middle

# Example I

Simulating Means and Medians

---

# When to use MC?

- When it's difficult to analytically derive the sampling distribution
    * E.g., indirect effect, fit-indexes; Cohen's `\(d\)`, *SE*s of estimators
- When required assumptions are violated
    * E.g., normality, large sample
    * Model is misspecified
    * Used to check __robustness__ of the estimator

---

# A Simulation Study is an Experiment

Experiment | Simulation
-----------|------------
Independent variables | Design factors 
Experimental conditions | Simulation conditions
Controlled variables | Other parameters
Procedure/Manipulation | Data generating model
Dependent variables | Evaluation criteria 
Substantive theory | Statistical theory
Participants | Replications

---
class: clear, center

(Sigal and Chalmers, 2016, Figure 1, p. 141)

---

# Design

Like experimental designs, conditions should be carefully chosen
- What to manipulate? Sample size? Effect size? Why?
    * Based on statistical theory and reasoning
    * E.g., Gauss-Markov theorem: regression coefficients are unbiased with 
    violations of distributional assumptions
- What levels? Why?
    * Needs to be realistic for empirical research
    * Maybe based on previous systematic reviews, 
    * Or a small review of your own
    
---

# Design (cont'd)

Full Factorial designs are most commonly used

Other alternatives include fractional factorial, random levels, etc
- See Skrondal (2000) for why they should be used more often

---

# Generate

- Starts with a statistical data generating model
    * E.g., `\(Y_i = \beta_0 + \beta_1 X_i + e_i,\quad e_i \overset{\textrm{i.i.d.}}{\sim} N(0, \sigma^2)\)`
        + Systematic (deterministic) component: `\(X_i\)`
        + Random (stochastic) component: `\(e_i\)`
        + Constants (parameters): `\(\beta_0\)`, `\(\beta_1\)`
    * `\(Y_i\)` completely determined by `\(X_i, e_i, \beta_0, \beta_1\)`
    
<div id="htmlwidget-daf636270d129b757355" style="width:504px;height:252px;" class="grViz html-widget"></div>
<script type="application/json" data-for="htmlwidget-daf636270d129b757355">{"x":{"diagram":"\ndigraph reg {\n\n  # a \"graph\" statement\n  graph [overlap = true, fontsize = 10]\n\n  # several \"node\" statements\n  node [shape = box,\n        fontname = Helvetica]\n  X; Y\n\n  node [shape = circle,\n        fixedsize = true] // sets as circles\n  e\n\n  # several \"edge\" statements\n  X -> Y\n  e -> Y\n  {rank = same; X; Y;}\n}\n","config":{"engine":"dot","options":null}},"evals":[],"jsHooks":[]}</script>

---

# Model-Based Simulation

---

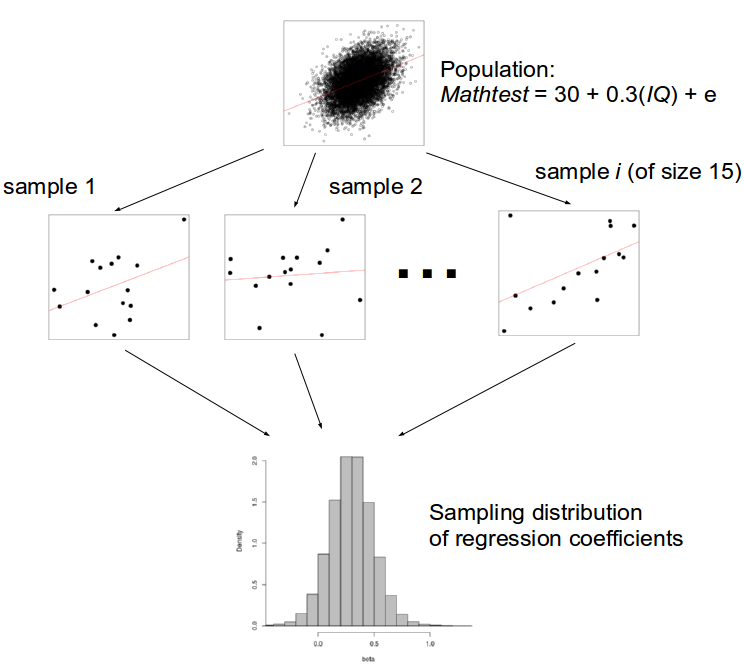
# Analyze

Analyze the simulated data using one or more analytic approaches
- Misspecification: study the impact when analytic model omits important aspects of data generating model
    * E.g., ignoring clustering
- Comparison of approaches
    * E.g., Maximum likelihood vs. multiple imputation for missing data handling

---

# Summarize (Evaluation Criteria)

- `\(\bar{\hat \theta}\)` = `\(\sum_{i = 1}^R \hat \theta_i / R\)`
- `\(\hat{\mathit{SD}}(\hat \theta)\)` = 
  `\(\sqrt{\frac{\sum_{i = 1}^R (\theta_i - \bar{\hat \theta})^2}{R}}\)`

For evaluating estimators:

- Bias
    * Raw: `\(\bar{\hat \theta} - \theta\)`
    * Relative: Bias / `\(\theta\)`
    * Standardized: Bias / `\(\hat{\mathit{SD}}(\hat \theta)\)`
- Relative efficiency (only for unbiased estimators)
    * `\(\mathrm{RE}(\hat \theta, \tilde \theta)\)` = `\(\frac{\hat{\mathrm{Var}}(\tilde \theta)}{\hat{\mathrm{Var}}(\hat \theta)}\)`

---

# Evaluation Criteria (cont'd)

For uncertainty estimators

- SE bias
    * Raw: `\(\overline{\mathit{SE}(\hat \theta)} - \hat{\mathit{SD}}(\hat \theta)\)`
    * Relative: SE bias / `\(\hat{\mathit{SD}}(\hat \theta)\)`

Combining bias and efficiency

- Mean squared error (MSE): `\(\frac{\sum_{i = 1}^R (\theta_i - \theta)^2}{R}\)`
    * Also = `\(\mathrm{Bias}^2 + \hat{\mathrm{Var}}(\hat \theta)\)`
    * Root MSE (RMSE) = `\(\sqrt{\mathrm{MSE}}\)`
- Mainly to compare 2+ estimators

---

# Evaluation Criteria (cont'd)

For statistical inferences:

- Power/Empirical Type I error rates
    * % with `\(p < \alpha\)` (usually `\(\alpha\)` = .05)
- Coverage of `\(C\)`% CI (e.g., `\(C\)` = 95%)
    * % where the sample CI contains `\(\theta\)`

---
class: clear

.font80[
Criterion | Cutoff | Citation
-----|-------|----------
Bias |.|.
Relative bias | ≤5% | Hoogland and Boomsma (1998)
Standardized bias | ≤.40 | Collins, Schafer, and Kam (2001)
*SE* bias |.|.
Relative *SE* bias | ≤10% | Hoogland and Boomsma (1998)
MSE |.|.
RMSE |.|.
Empirical Type I error (α = .05) | 2.5% - 7.5% | Bradley (1978)
Power |.|.
95% CI Coverage | 91%-98% | Muthén and Muthén (2002)
]

---

# Results

Just like you're analyzing real data

- Plots, figures
- ANOVA, regression
    * E.g., 3 (sample size) × 4 (parameter values) 2 (models) design: 2 between
    factors and 1 within factor

---
class: inverse, center, middle

# Example II

Simulation Example on Structural Equation Modeling

---

# Number of Replications

Should be justified rather than relying on rule of thumbs

## Why Does MC Work?

- Law of large number
    * `\(\sum_{i = 1}^R T_i / R \overset{p}{\to} \theta\)`
- When `\(R\)` is large, 
    + the empirical distribution `\(\hat{F}(t)\)` converges to the true sampling distribution `\(F(t)\)`.

---

# Number of Replications (cont'd)

## How Good is the Approximation

- Monte Carlo (MC) Error 
    * Like standard error (SE) for a point estimate
- For expectations (e.g., bias)
    * MC Error = `\(\hat{\mathit{SD}}(\hat \theta) / \sqrt{R}\)`

E.g., if one wants the MC error to be ≤2.5% of the sampling variability, 
_R_ needs to be 1 / `\(.025^2\)` = 1,600

---

# Number of Replications (cont'd)

For power (also Type I error) and CI coverage, 
* MC Error = `\(\sqrt{\frac{p (1 - p)}{R}}\)`

E.g., with _R_ = 250, and empirical Type I error = 5%,

```r
sqrt((.05 * (1 - .05)) / 250)
```

```
## [1] 0.01378405
```
So _R_ should be increase for more precise estimates

---

# Reporting MC Results

![](images/Boomsma_table1.png)

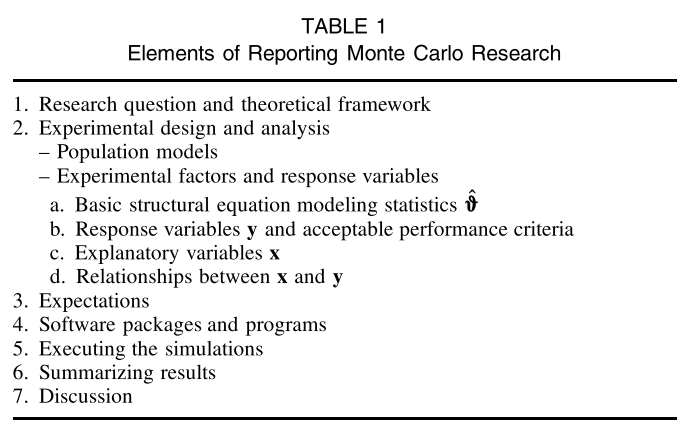
(Boomsma, 2013, Table 1, p. 521)

See Boomsma (2013), Table 2, p. 526 for a checklist

---

# Efficiency tips

- Things that don't change should be outside of a loop
- Initialize place holders when using for-loops
- [Vectorize](https://adv-r.hadley.nz/perf-improve.html#vectorise)
- Strip out unnecessary computations
- Parallel computing (using the `future` package)

---

# Other topics not covered

- Error handling
- Assessing convergence
- Debugging
- Interfacing with other software (e.g., Mplus, LISREL, HLM)

---

# Further Readings

Carsey and Harden (2014) for a gentle introduction

Chalmers (2019) and Sigal and Chalmers (2016) for using the R
package `SimDesign`

Harwell, Kohli, and Peralta-Torres (2018) for a review of design and reporting practices

Skrondal (2000), Serlin (2000), and 
Bandalos and Leite (2013) for additional topics

---

class: inverse, center, middle

# Thanks!

---

# References

.font70[
Bandalos, D. L. and W. Leite (2013). "Use of Monte Carlo studies
in structural equation modeling research". In: _Structural
equation modeling. A second course_. Ed. by G. R. Hancock and R.
O. Mueller. 2nd ed. Charlotte, NC: Information Age, pp. 625-666.

Boomsma, A. (2013). "Reporting Monte Carlo studies in structural
equation modeling". In: _Structural Equation Modeling_. _A
Multidisciplinary Journal_ 20, pp. 518-540. DOI:
[10.1080/10705511.2013.797839](https://doi.org/10.1080%2F10705511.2013.797839).

Bradley, J. V. (1978). "Robustness?" In: _British Journal of
Mathematical and Statistical Psychology_ 31, pp. 144-152. DOI:
[10.1111/j.2044-8317.1978.tb00581.x](https://doi.org/10.1111%2Fj.2044-8317.1978.tb00581.x).

Carsey, T. M. and J. J. Harden (2014). _Monte Carlo Simulation and
resampling. Methods for social science_. Thousand Oaks, CA: Sage.

Chalmers, P. (2019). _SimDesign: Structure for Organizing Monte
Carlo Simulation Designs_. R package version 1.13. URL:
[https://CRAN.R-project.org/package=SimDesign](https://CRAN.R-project.org/package=SimDesign).
]

---

# References (cont'd)

.font70[
Collins, L. M, J. L. Schafer, and C. Kam (2001). "A comparison of
inclusive and restrictive strategies in modern missing data
procedures". In: _Psychological Methods_ 6, pp. 330-351. DOI:
[10.1037//1082-989X.6.4.330](https://doi.org/10.1037%2F%2F1082-989X.6.4.330).

Harwell, M, N. Kohli, and Y. Peralta-Torres (2018). "A survey of
reporting practices of computer simulation studies in statistical
research". In: _The American Statistician_ 72, pp. 321-327. ISSN:
0003-1305. DOI:
[10.1080/00031305.2017.1342692](https://doi.org/10.1080%2F00031305.2017.1342692).

Hoogland, J. J. and A. Boomsma (1998). "Robustness studies in
covariance structure modeling". In: _Sociological Methods &
Research_ 26, pp. 329-367. DOI:
[10.1177/0049124198026003003](https://doi.org/10.1177%2F0049124198026003003).

Muthén, L. K. and B. O. Muthén (2002). "How to use a Monte Carlo
study to decide on sample size and determine power". In:
_Structural Equation Modeling_ 9, pp. 599-620. DOI:
[10.1207/S15328007SEM0904_8](https://doi.org/10.1207%2FS15328007SEM0904_8).

Serlin, R. C. (2000). "Testing for robustness in Monte Carlo
studies". In: _Psychological Methods_ 5, pp. 230-240. DOI:
[10.1037//1082-989X.5.2.230](https://doi.org/10.1037%2F%2F1082-989X.5.2.230).
]

---

# References (cont'd)

.font70[
Sigal, M. J. and R. P. Chalmers (2016). "Play it again: Teaching
statistics with Monte Carlo simulation". In: _Journal of
Statistics Education_ 24.3, pp. 136-156. ISSN: 1069-1898. DOI:
[10.1080/10691898.2016.1246953](https://doi.org/10.1080%2F10691898.2016.1246953).
URL: [https://doi.org/10.1080/10691898.2016.1246953
https://www.tandfonline.com/doi/full/10.1080/10691898.2016.1246953](https://doi.org/10.1080/10691898.2016.1246953
https://www.tandfonline.com/doi/full/10.1080/10691898.2016.1246953).

Skrondal, A. (2000). "Design and analysis of Monte Carlo
experiments". In: _Multivariate Behavioral Research_ 35, pp.
137-167. DOI:
[10.1207/S15327906MBR3502_1](https://doi.org/10.1207%2FS15327906MBR3502_1).
]